Learning activity 1.2: Exploring relative motion

Explore this!

Let's review some key terms that are associated with motion. Explore the following video in which Paul Andersen describes motion as the movement of an object over time. Displacement, velocity and acceleration are all defined. An experiment in motion is used to calculate velocity and acceleration of a tennis ball.

All motion is relative and understanding how to utilize the tools from our previous learning activity will help you analyze the world around you.

Think

Consider the following questions:

Do we all observe the world in the same way?
Are we moving the way we think we are moving?
Does your physical description depend on what I am doing?

Crossing a river

You are taking part in a canoe race, or canoe sprint across a river. Canoe sprint or canoe race is a sport which athletes race canoes or kayaks in the water, such as lake or river.

You need to reach the other side first, regardless of where you land on the opposite side.

Think

How can you do this? Consider the following questions:

Should you aim to cross the river somewhat upstream, to counteract the effect of the current?
Should you aim to cross somewhat downstream, to travel with the current?
Should you travel straight across, perpendicular to the current?

By the end of this learning activity, you will know these answers. After studying the learning activity on relative motion and frames of reference, you will be able to figure out how to win this race!

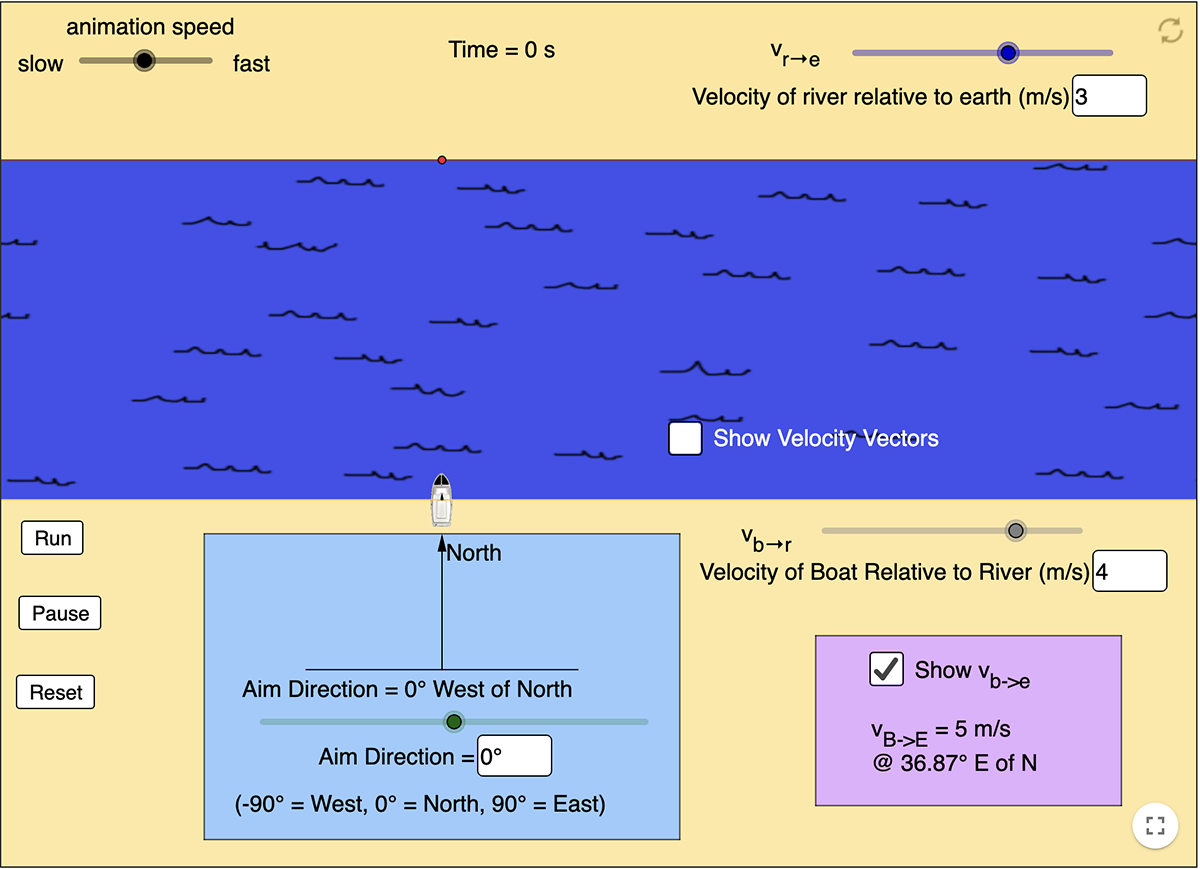
Simulation to explore vector velocity and the horizontal and vertical components

Start

Before learning about the concepts behind relative motion, let’s investigate if you can get the boat across a river in the following simulation.

Instructions:

You can adjust two different aspects of the motion of boat:

The direction of the boat, and
The velocity of the boat relative to the river.

You can also adjust the river speed (current). By changing these values, try to get the boat across the river directly to the other side (to the point with the red dot).

The following simulation is a boat crossing a river. Adjust the direction the boat is aimed, the boat’s velocity relative to the river, and the river’s velocity relative to the earth.

Press start to launch the application. Once you have changed a variable, press the [Run] button to observe the boat's trip across the river. Press [Reset] to return to the original conditions and adjust a different variable.

Relative motion

The effect of the wind causes the motion of a plane to change. Headwinds, tailwinds, and crosswinds are all important to pilots as they navigate to a desired destination. Accurate and precise navigation requires an understanding of the fact that direction of motion of a plane can change as a result of relative forces, for example, it can change due to the direction and velocity of the wind with respect to the ground.

In the case of the simulation of the boat crossing, adjusting to the current speed is also imperative while navigating bodies of water.

Definition

Frame of reference:

The point of view from which observations and measurements of motion are made. It is a coordinate system relative to the motion being observed.

Coordinate system:

A representation of a position in space. The most common coordinate system is the rectangular coordinate system or Cartesian coordinate system. It’s used to determine the distance between points.

Note: Establishing a frame of reference for motion is important. It clarifies how the motion appears, relative to a set of coordinates.

Explore this!

Explore the following animation video and notice the importance of establishing a frame of reference. Consider the following question while viewing the video:

Is the pathway of motion for the ball, as observed by the sailor, the same as the pathway of motion for the ball as observed by the person on shore?

Consider each frame of reference from the animation and describe the ball’s path of motion relative to each observer.

Notebook

You can use your notebook to complete each of the following questions. Compare your work with the suggested answers to check your understanding.

Describe the path of motion relative to the sailor:

The sailor is stationary, with respect to the boat. He is initially holding the ball stationary, relative to the boat. When he drops the ball, it falls straight downward, with respect to him and the boat. He observes a vertical downward path relative to the boat.

Describe the path of motion relative to the observer on shore:

Initially the sailor, the ball and boat are all moving to the right, relative to the shore. The ball has the same horizontal velocity when it is dropped. Therefore, relative to the observer on the shore, the ball is moving to the right, as it moves downward.

Frames of reference are important in clarifying your observation and measurements of motion, especially when one frame of reference is in motion, relative to another.

In the animation, you will have noticed that the ball appears to be dropped straight downwards relative to the passengers on the boat with the boat moving relative to the shore. However, to an observer on the shore, the ball appears to have a different trajectory, one that has a horizontal velocity. When dealing with motion in various frames of references, you will consider the concept of relative velocity.

Definition

Relative velocity: the velocity of an object relative to its frame of reference.

Problem solving with relative velocity involves an analysis of the motion of an object within a frame of reference that is also in motion. Consider, for example, the ball and boat. Because the boat was moving, the total (also known as net) velocity of the ball relative to the ground would be the following:

$\vec{V_{n e t}} = \vec{V_{b a l l}} + \vec{V_{b o a t}}$

Recall, the plus sign (+) actually describes how the vectors are connected - in this case, added together. It means “connect the head of the first vector to the tail of the second vector.” This can also be represented by the following diagram of the vectors where V_ball is added with V_boat to get V_net.

V ball (vertical) and V boat (horizontal) combined vectors give the resulting vector.

While solving relative velocity problems, it will be helpful to record subscripts with your variables. This technique can help you to reason through these problems. Using this method, each variable in a relative motion problem is given two subscripts. The first subscript refers to the object being discussed and the second refers to its frame of reference.

An illustration of a boat crossing a river upstream, against the current.

Example

To understand this use of subscripts, consider a situation where there is a boat travelling on a river in which there is a current, and you want to know the velocity of the boat with respect to the shore. The following table explains how and when subscript to use.

We can use “B” to represent the boat, “W” to represent the water, and “G” to represent the ground.

To represent the...	We use the variable...
Velocity of the boat with respect to the water (i.e. the heading of the boat).	$\vec{v_{B W}}$
Velocity of the water with respect to the ground (i.e. the speed and direction of the current).	$\vec{v_{W G}}$
Velocity of the boat with respect to the ground (i.e. what an observer on the shore would notice). It is the net velocity, which is the sum of the other two velocities.	$\vec{v_{B G}}$

The following equation will help you find the total velocity of the boat relative to the ground.

Notice the subscript rules from the previous table applied as well.

Graphic representation for the subscripts of velocities in different frames of reference

Relative motion examples

The next four examples show various scenarios that involve relative motion. The first two involve collinear vectors (vectors that share the same line) and the last two are based on non-collinear vectors (vectors that do not fall on the same line). Each of the examples will use the following basic scenario:

Alex (they/them), a canoeist, can consistently row to maintain a speed of 1.5 m/s in still water. Right now, Alex is travelling in a river that has a current of 1.0 m/s [S].

Let’s examine at four unique examples:

Adding collinear vectors.
Adding collinear vectors with opposite directions.
Adding non-collinear vectors that form a right-angled triangle.
Adding non-collinear vectors that do not form a right-angled triangle.

The following two examples will help to clarify the concepts involving addition of collinear vectors.

Example 1: Adding collinear vectors

If the canoe is heading downstream in the river, what will Alex’s velocity be, relative to a stationary observer on the shore (ground)?

Let w= water; c = canoe; s = shore

River current is velocity of water relative to the shore: $\vec{v_{W S}} = 1.0 \frac{m}{s} [S]$

Canoe’s velocity relative to water: $\vec{v_{C W}} = 1.5 \frac{m}{s} [S]$

$\vec{v_{C S}} = ?$

Step 1 – Draw a vector diagram that includes a designated direction to represent the addition of the two vectors.

Since these two vectors have the same direction, they can be added together.

Step 2 – Add the collinear vectors.

The following is a vector diagram for the scenario:

$\vec{v_{C S}} = \vec{v_{C W}} + \vec{v_{W S}}$

(since South has been chosen as the positive direction, these vectors can be added)

$\vec{v_{C S}} = 1.5 m / s [S] + 1.0 m / s [S]$

$\vec{v_{C S}} = 2.5 m / s [S]$

Alex’s velocity relative to an observer on shore will be 2.5 m/s [S].

Example 2: Adding collinear vectors with opposite directions

If the canoe is heading upstream in the river, what will Alex’s velocity be, according to an observer on the shore?

Let w = water; c = canoe; s = shore

River current is velocity of water relative to the shore: $\vec{v_{W S}} = 1.0 \frac{m}{s} [S]$

Canoe’s velocity relative to water: $\vec{v_{C W}} = 1.5 \frac{m}{s} [N]$

(Alex is moving upstream, meaning against the current)

$\vec{v_{C S}} = ?$

Step 1 – Draw a vector diagram that includes a designated direction to represent the addition of the two vectors.

If the north direction is chosen as the positive direction then, there are collinear vectors that have opposing directions. To add the current vector, represent 1.0 m/s [S] as -1.0 m/s [N].

Step 2 – Add the collinear vectors.

The following is a vector diagram of the scenario:

$\vec{v_{C S}} = \vec{v_{C W}} + \vec{v_{W S}}$

(since North has been chosen as the positive direction, these vectors can be added)

$\vec{v_{C S}} = 1.5 m / s [N] + (- 1.0 m / s [N])$

$\vec{v_{C S}} = 1.5 m / s [N] - 1.0 m / s [N]$

$\vec{v_{C S}} = 0.5 m / s [N]$

Alex’s velocity relative to an observer on shore will be 0.5 m/s [N].

Notebook

You can use your notebook to complete each of the following questions on relative velocity of collinear vectors. Compare your work with the suggested answers to check your understanding.

Rashida (she/her) needs to get her load of produce from home to the market, which is 15 km downstream. There is a current of 8.0 km/h flowing downstream. Rashida’s launch can travel at 25 km/h in still water.

Find Rashida’s velocity relative to the water as she travels downstream to the market.

$\vec{v_{b w}}$ = 25 km/h [downstream]

Find Rashida’s velocity relative to the ground as she travels downstream to the market.

$\vec{v_{B G}} = \vec{v_{B W}} + \vec{v_{W G}}$ = 8 km/h[downstream] + 25 km/h [downstream] = 33 km/h [downstream]

How long will it take Rashida to reach the market?

Since she has a constant velocity with a magnitude of 33km/h and a distance of 15 km to cover.

$t = \frac{d}{v} = \frac{15 km/h}{33 km/h} = 0.45 h$

Find Rashida’s velocity as she travels back home (upstream from the market).

$\vec{v_{B G}} = \vec{v_{B W}} + \vec{v_{W G}}$

$\vec{v_{B G}} =$ 8 km/h [downstream] + 25 km/h [upstream]

$\vec{v_{B G}} =$ - 8 km/h [upstream] + 25 km/h [upstream]

$\vec{v_{B G}} =$ 17 km/h [upstream]

Note: The velocities were subtracted as the directions were opposite.

How long will it take Rashida to get home from the market?

Since she has a constant velocity with a magnitude of 17 km/h and a distance of 15 km to cover.

$t = \frac{d}{v} = \frac{15 km/h}{17 km/h} = 0.88 h$

The following two examples will help to clarify the concepts involving addition of non-collinear vectors.

Example 3: Adding non-collinear vectors that form a right-angled triangle

Let's return to Alex’s canoe trip scenario.

If the canoe travels west, directly across the river perpendicular to the current, what will Alex’s velocity be, according to an observer on the shore?

Let w = water; c = canoe; s = shore

River current is velocity of water relative to the shore: $\vec{v_{W S}} = 1.0 \frac{m}{s} [S]$

Canoe’s velocity relative to water $\vec{v_{C W}} = 1.5 \frac{m}{s} [W]$

(Alex paddles perpendicular to the river current).

$\vec{v_{C S}} = ?$

Step 1 – Draw a vector diagram that includes a designated direction to represent the addition of the two vectors.

In this case the vectors act at right angles to one another along the south and west directions.

Step 2 – Use the Pythagorean theorem to determine the magnitude of the resultant vector.

Step 3 – Determine the direction of the resultant vector using a trigonometric function. The tangent function is the best choice because these values were given (as opposed to calculated).

The following is a vector diagram of the scenario:

The resultant vector, $\vec{v_{C S}}$ , is the velocity of the canoe relative to the shore. It is found by adding the velocity of water relative to the shore and the canoe’s velocity relative to water:

$\vec{v_{C S}} = \vec{v_{C W}} + \vec{v_{W S}}$

Determine the magnitude (scalar value) of the resultant vector

${{|v_{c s}|}^{2} = |v_{c w}|}^{2} + {|v_{w s}|}^{2}$

${{|v_{c s}|}^{2} = (1.5 \frac{m}{s})}^{2} + {(1.0 \frac{m}{s})}^{2}$

$|v_{c s}| = \sqrt{({1.5 \frac{m}{s})}^{2} + {(1.0 \frac{m}{s})}^{2}}$

$|v_{c s}| = 1.8 m / s$ (rounded to 2 significant figures)

To find the angle:

$t a n θ = \frac{| v_{w s} |}{| v_{c w} |}$

$t a n θ = \frac{1.0 m / s}{1.5 m / s}$

$θ = {t a n}^{- 1} (\frac{1.0 m / s}{1.5 m / s})$

$θ = 33.69 °$

$θ = 34 °$ (rounded to 2 significant digits)

Alex’s velocity relative to an observer on shore will be 1.8 m/s [W 34° S].

Example 4: Adding non-collinear vectors that do not form a right-angled triangle

Now, Alex heads his canoe at an angle of 35° upstream. What will Alex’s velocity be, this time, with respect to the observer on the shore?

Let w = water; c = canoe; s = shore

River current is velocity of water relative to the shore: $\vec{v_{W S}} = 1.0 \frac{m}{s} [S]$

Canoe’s velocity relative to water: $\vec{v_{C W}} = 1.5 \frac{m}{s} [W 35 ° N]$

(Alex’s direction 35° North of West)

$\vec{v_{C S}} = ?$

Step 1 – Draw a vector diagram that includes a designated direction to represent the addition of the two vectors.

If the north direction is chosen as the positive direction then, neither of the two vectors are along a directional axis. In other words, the two vectors are non-collinear vectors, and each have both an x-component and a y-component.

Step 2 – Resolve each vector into its components.

Step 3 – Separately add the x-component and y-component vectors together.

Step 4 – Use the Pythagorean theorem to determine the magnitude of the resultant vector.

Step 5 – Determine the direction of the resultant vector using a trigonometric function.

The following is a vector diagram of the scenario:

To determine the value for x-components( $\vec{v_{{C W}_{x}}}, \vec{v_{{W S}_{x}}}, \vec{v_{{C S}_{x}}}$ ):

$v_{{c w}_{x}} = v_{c w} c o s 35 °$

$\vec{v_{{C W}_{x}}} = (1.5 m / s) (c o s 35 °)$

$\vec{v_{{C W}_{x}}} = (1.23 m / s)$ (1 extra digit)

$v_{{w s}_{x}} = 0 m / s$

$v_{{c s}_{x}} = v_{{c w}_{x}} + v_{{w s}_{x}}$

$\vec{v_{{C S}_{x}}} = 1.229 m / s + 0 m / s$

$\vec{v_{{C S}_{x}}} = 1.23 m / s [W]$ (rounded to 3 significant figures - one extra for intermediate answers)

Recall that for intermediate answers, always keep one more significant figure for your value.

To determine the value for y-components ( $\vec{v_{{C W}_{y}}}, \vec{v_{{W S}_{y}}}, \vec{v_{{C S}_{y}}}$ ):

$v_{{c w}_{y}} = v_{c w} s i n 35 °$

$\vec{v_{{C W}_{y}}} = (1.5 m / s) (s i n 35 °)$

$\vec{v_{{C W}_{y}}} = 0.860 m / s [N]$ (rounded to 3 significant figures - one extra for intermediate answers)

$\vec{v_{{C W}_{y}}} v_{{w s}_{y}} = 1.0 m / s [S]$

$v_{{c s}_{y}} = v_{{c w}_{y}} + v_{{w s}_{y}}$

$\vec{v_{{C S}_{y}}} = 0.860 m / s [N] + 1.0 m / s [S]$

$\vec{v_{{C S}_{y}}} = 0.860 m / s [N] + (- 1.0 m / s [N])$

Since north and west were chosen as the positive direction, the [S] vector direction is converted to a north direction vector to allow for vector addition.

$\vec{v_{{C S}_{y}}} = - 0.1396 m / s [N]$ or $0.1396 m / s [S]$

$\vec{v_{{C S}_{y}}} = 0.14 m / s [S]$ (rounded to 2 significant digits)

The following diagram (not to scale) is for the resultant vector with the values of x and y components that were just solved.

Now the to determine the magnitude (scalar value) of the resultant vector using the Pythagorean theorem can be used:

${{|v_{c s}|}^{2} = |v_{{c s}_{x}}|}^{2} + {|v_{{c s}_{y}}|}^{2} {{|v_{c s}|}^{2} = (1.23 \frac{m}{s})}^{2} + {(0.140 \frac{m}{s})}^{2} |v_{c s}| = \sqrt{({1.23 \frac{m}{s})}^{2} + {(0.140 \frac{m}{s})}^{2}}$

$|v_{c s}| =$ 1.2 m/s (rounded to 2 significant figures)

To find the angle:

$t a n θ = \frac{| v_{{c s}_{y}} |}{| v_{{c s}_{x}} |}$

$t a n θ = \frac{0.1396 \frac{m}{s}}{1.229 \frac{m}{s}}$

$θ = {t a n}^{- 1} (\frac{0.1396 \frac{m}{s}}{1.229 \frac{m}{s}})$

$θ = 6.48 °$

$θ = 6.5 °$ (rounded to 2 significant digits)

Thus, the vector direction is [W6.5°S].

Alex’s velocity relative to an observer on shore will be 1.2 m/s [W 6.5°S].

Discover more

Use your preferred search engine and search for terms “significant digits” and “physics” to review the rules regarding significant digits. These search terms are provided as suggestions only. You are encouraged to search for additional resources to support your understanding.

Notebook

Answer the following practice questions in your notebook on relative velocity of non-collinear vectors. Compare your work with the answer sheet afterwards to check your understanding.

Muntaha (she/hers) paddles 2.8 m/s [W] from her dock, but there is a current in the lake moving at 1.5 m/s [S]. Find her resultant velocity as observed by a person on shore.
Eric(he/they) wants to fly from Toronto to North Bay, a displacement of 320 km [N]. Eric flies at 120 km/h [N], but there is a wind of 40 km/h blowing from the east.

$\vec{v_{P G}}$ = Velocity of plane relative to ground (groundspeed) = ?

$\vec{v_{P A}}$ = Velocity of plane relative to the air (airspeed) = 120 km/h [N]

$\vec{v_{A G}}$ = Velocity of air relative to ground (wind speed) = 40 km/h [W]

What is Eric’s resultant velocity as observed by a person on the ground?
If Eric follows this flight path, will he reach the destination?
Make a sketch to show the path that Eric should have initially followed, in order to fly directly to the desired destination.
At what angle should he aim the plane, so that he can follow this new path?
What is Eric's final velocity, if he follows this new path?
How long will it take Eric to get to North Bay, if he follows this new route?

Check your answers for questions related to Muntaha and Eric with this answer sheet(Opens in New Window).

Join the discussion

There are many mathematicians and scientists that have contributed to the field of physics; however, their names may not be mentioned, but their contributions become part of the concepts and theories that you will encounter in this course. Katherine Johnson was the first African American woman to work as a scientist for NASA. She was able to use her extensive knowledge of geometry for space travel and contributed to Apollo 11 mission to the moon, 1969. Her mathematical contributions in space exploration help to revolutionize mathematics in physics and space. Many of the concepts and mathematical equations found in this unit has been developed and contributed by many mathematicians and scientists with diverse backgrounds.

Source: https://en.wikipedia.org/wiki/Katherine_Johnson

In this activity, you will research either a mathematician or scientist and their contribution to physics unit of dynamics. Please include the following criteria:

Name of the mathematician/scientist (include a picture).
Summarize the mathematician/scientist and their contribution.
How does their contribution impact what you are currently learning in this unit.

Once you have completed your research, post the information in the discussion forum. Review the information that has been posted, comment on what you find interesting.

Finding the heading of a moving object

In the following example, you will be given the canoe’s velocity relative to the shore (e.g. an observer on the ground) and the current speed and direction. You will gain an understanding on how to find the canoe’s velocity with respect to the water using trigonometry.

Example

From the previous section, let’s reexamine the canoeing scenario, suppose that Alex, in the canoe, must cross the river to a point on the west bank, directly opposite the starting point. It was found that, relative to the shore, Alex was moving at 1.12 m/s in the canoe as illustrated in the following diagram. What is the velocity of the canoe relative to the water? At what angle must Alex be able to head upstream?

Illustration of the canoeing scenario described in the word problem.

The canoe must follow a path due west, perpendicular to the riverbank.

$\vec{v_{W S}} = 1.0 \frac{m}{s} [S]$

$\vec{v_{C S}} = 1.12 \frac{m}{s} [W]$

$\vec{v_{C W}} = ?$

(The direction and speed required to maintain a path due west.)

The following is a vector diagram of the scenario:

To find the angle:

$\tan θ = \frac{1 m/s}{1.12 m/s}$

$θ = {41.8}^{\circ}$

Determine the magnitude of the resultant vector:

$|\vec{v_{C S}}| = \sqrt{{|\vec{v_{C W}}|}^{2} + {|\vec{v_{W S}}|}^{2}}$

$|\vec{v_{C S}}| = 1.5 \frac{m}{s}$

To maintain a path due west across the river, Alex would have to direct the canoe 42° upstream, at a speed of 1.5 m/s.

There is an alternate solution for this example using vector subtraction methods.

Vector subtraction and relative velocity

Let’s go back to the same example. You will explore how to use vector subtraction to find the velocity of the canoe with respect to the water. Examine the following diagram:

Triangular vector diagram where vector CS & vector WS are meeting. Resulting vector is CW

Earlier in Learning Activity 1.1 you acquired knowledge to determine relative velocities using vector addition. For the scenario when you add the vectors head to tail the result is:

$\vec{v_{C S}} = \vec{v_{C W}} + \vec{v_{W S}}$

In this example $\vec{v_{C S}}$ is already known. It is the velocity of the canoe relative to the water ( $\vec{v_{C W}}$ ) that is unknown. If you rearrange this equation and isolate, $\vec{v_{C W}}$ then:

$\vec{v_{C W}} = \vec{v_{C S}} - \vec{v_{W S}}$

It is standard practice to add vectors. Note that in physics, a negative sign associated with a vector simply means “in the opposite direction”. A negative vector means you take the original vector and point it in exactly the opposite direction, ( $180 °$ from its initial position) so, the equation becomes:

$\vec{v_{C W}} = \vec{v_{C S}} + (- \vec{v_{W S}})$

and $(- \vec{v_{W S}})$ simply means: −1.0 m/s [S] is 1.0 m/s [N].

Therefore, after substituting this value the formula becomes the following:

$\vec{v_{C W}} = \vec{v_{C S}} + 1.0 m / s [N]$

So, now you can use the Pythagorean theorem to determine the magnitude of $\vec{v_{C W}}$ and the tangent function to determine the angle of direction.

${| {v_{c w} |}^{2} = | v_{c s} |}^{2} + {(1.0 m/s)}^{2} {| {v_{c w} |}^{2} = (1.12 m/s)}^{2} + {(1.0 m/s)}^{2} | v_{c w} | = \sqrt{{(1.12 m/s)}^{2} + {(1.0 m/s)}^{2}} | v_{c w} | = 1.5 m / s$

(rounded to 2 significant figures)

Angle of direction:

$\tan θ = \frac{|v_{w s}|}{|v_{c s}|}$

$\tan θ = \frac{1.0 m / s}{1.12 m / s}$

$θ = \tan^{- 1} (\frac{1.0 m / s}{1.12 m / s})$

$θ = 42 °$ (rounded to 2 significant figures)

Join the discussion

You will now have the opportunity to have more practice with relative motion using vector subtraction. In this discussion forum, you will post a question similar to the examples in this learning activity. Once you post your question in the forum, answer a question posted by a classmate. When one of your classmates provides the solution to your posted question, check their answer, and provide feedback, if applicable. If there are any tips that you have used to solve these problems post in this discussion forum.

Assessment Opportunity

Please answer the following questions in your notebooks. Once you have completed these questions please submit to check for understanding on solving relative velocity problems. Your teacher will provide descriptive feedback.

An airplane flies with an airspeed of 50.0 m/s [E 40° N]. If the velocity of the airplane, according to an observer on the ground, is 30.0 m/s [SE], what is the wind velocity?
Examine the scenario introduced at the beginning of the learning activity, taking into consideration what you have learned so far about relative velocities. The scenario involved a canoe race across a river. Imagine, now, that you are taking part in the race and desperately want to reach the other side first, regardless of where you land on the opposite side. How can you do it?
- Should you aim to cross the river somewhat upstream, to counteract the effect of the current?
- Should you aim to cross somewhat downstream, to travel with the current?
- Should you travel straight across, perpendicular to the current?

Part 1: Reflect on your learning

Return to the simulation that you started the learning activity with, but this time with knowledge of how the boat’s velocity with respect to the ground (i.e. observed by a person standing on the shore) is the vector sum of the boat’s velocity with respect to the water and the water’s velocity with respect to the ground.

Start

The velocity vectors can be appear within the stimulation by clicking on the “Show velocity vectors” checkbox. Press on and/or adjust the other following features as well:

Animation speed: slow to fast [toggle]
Velocity of river relative to the earth (m/s) [toggle]
Aim direction [toggle]
Velocity of the boat relative to the river (m/s) [toggle]
Show velocity formula [checkbox]

Using the method shown in this learning activity, head the boat out perpendicularly across the river, and calculate the direction and velocity of the boat with respect to the ground in your notebook. What you calculate should be very similar to what the simulation reveals.

Part 2: Summarize your learning: Concept map

To better understand how each of the concepts in this learning activity relate to each other, you will organize the concepts in a graphic organizer.

You will be completing a concept map after each learning activity. At the end of each unit, you will combine them to provide a comprehensive graphic organizer that summarizes the concepts of the unit.

Notebook

Review your concept map from Learning Activity 1.1 and then create your concept map for this learning activity in your notebook. At this time, you can either create a new, separate concept map for this learning activity or add these terms to your previous concept map.

You will use a concept map to organize the following terms based on their relationships with each other.

Terms to include: (may be used more than once)

relative motion
adding vectors
subtracting vectors
frames of reference

Add any other terms that you think are important from this learning activity.

Explore this!

Think

Crossing a river

Think

Instructions:

Relative motion

Definition

Frame of reference:

Coordinate system:

Explore this!

Notebook

Definition

Example

Relative motion examples

Example 1: Adding collinear vectors

Given

Required

Analysis

Solution

Summary

Example 2: Adding collinear vectors with opposite directions

Given

Required

Analysis

Solution

Summary

Notebook

Example 3: Adding non-collinear vectors that form a right-angled triangle

Given

Required

Analysis

Solution

Summary

Example 4: Adding non-collinear vectors that do not form a right-angled triangle

Given

Required

Analysis

Solution

Summary

Discover more

Notebook

Join the discussion

Finding the heading of a moving object

Example

Given

Required

Analysis

Solution

Summary

Vector subtraction and relative velocity

Join the discussion

Assessment Opportunity

Part 1: Reflect on your learning

Part 2: Summarize your learning: Concept map

Notebook