Introduction

The properties of triangles have been used for centuries to solve all kinds of problems. Mathematicians have been around for thousands of years in different parts of the world and as a result, we have the pyramids of Ancient Egypt. Another place where mathematicians could be found early on is in Greece. The word “trigonometry” comes from a combination of the Greek words for “three,” “angle,” and “measurement.” As early as 140 BCE, Greek mathematicians were using triangles to solve problems in astronomy and navigation. In this learning activity, you will build on the properties of similar triangles to discover a much more powerful set of tools called the trigonometric ratios (or trig ratios, for short).
What you will learn
After completing this learning activity, you will be able to:
- define the formulas for the primary trigonometric ratios in terms of the sides of a right triangle
- solve for unknown sides and angles in right triangles using the primary trigonometric ratios
Right triangles

When working with right triangles, it is important to label them correctly and consistently. This way, the properties you discover in this learning activity will always apply correctly to the problems you are trying to solve.
Also, following consistent rules makes it easier to communicate your ideas to other people, in the same way that grammar and punctuation are important when you write a paragraph.
In a right triangle:
- The hypotenuse is the side across from the 90° angle.
- The reference angle is either of the other two angles (never the 90° angle).
- The opposite side is the side across from the reference angle.
- The adjacent side is the side between the reference angle and the 90° angle.
Labelling triangles
The labelling system mentioned previously is explored here in :
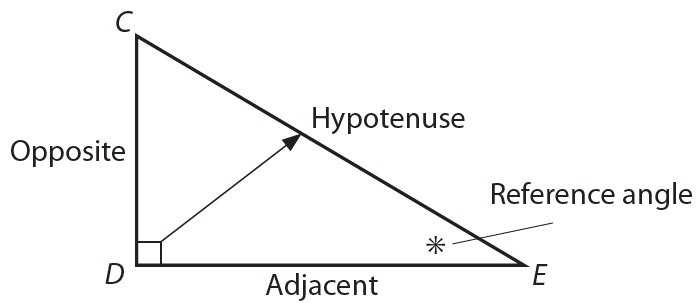
- is the angle, so is the hypotenuse.
- has been selected as the reference angle (*), so is the opposite side.
- is between the reference angle and the angle, so is the adjacent side.
Now consider :
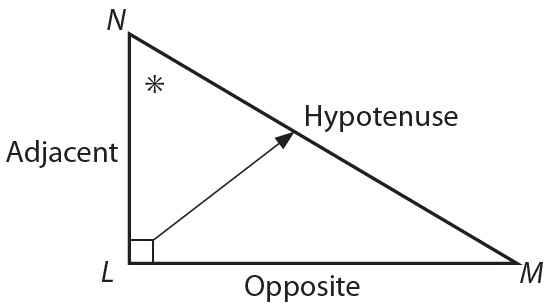
- is the angle, so is the hypotenuse.
- has been selected as the reference angle (*), so is the opposite side.
- is between the reference angle and the angle, so is the adjacent side.
Try it!
Use the diagram of the triangle to answer the following questions.

Note: Assume is the reference angle in the triangle.
Use the diagram of the triangle to answer the following questions.

Note: Assume is the reference angle in the triangle.
Exploring ratios in similar right triangles
Recall what you learned about similar triangles:
- Corresponding angles are equal.
- Corresponding sides are in the same ratio.
Explore this!
Let’s do a quick review before moving on to the next topic. Explore the following video to investigate the ratios of the sides in two similar right triangles.
Exploring the primary trigonometric ratios
In the previous learning activity, you explored similar triangles and found that as the triangles were altered in shape and size while maintaining their similarity, the following two facts could always be relied on:
- Corresponding angles in similar triangles are equal.
- All pairs of corresponding sides of similar triangles are in the same ratio.

Defining SINE, COSINE, and TANGENT
Recall that similar triangles have ratios. So do the sides in a right triangle, and in a right triangle these new ratios have names!
Explore this!
Explore the following video about the three primary trigonometric ratios: sine, cosine, and tangent.
Try it!
Let’s try a few examples. Use the mnemonic “SOH – CAH – TOA” to help you recall the names of the ratios and the sides being compared.
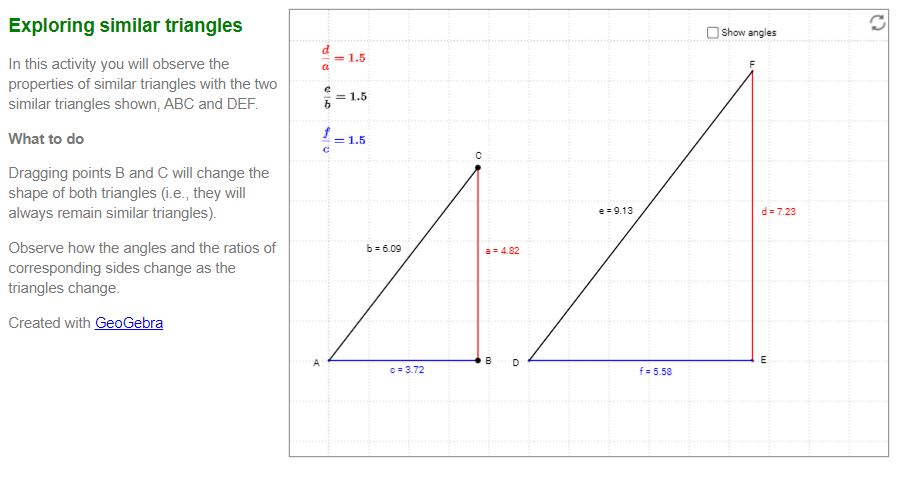
Investigating similar triangles
Portfolio
There is a pair of similar triangles in the following graphing app. Use the app to drag any of the vertices. This will change the dimensions of the sides as well as the measure of the angles. What do you notice? Complete the following worksheet(Opens in new window) and submit it for feedback.
What did you discover?
You should be able to confirm that no matter how you changed the triangles, the following things always held true:
- The corresponding angles of the similar triangles and were always equal to each other.
- The ratio of all corresponding sides was always the same for all sides.
- The primary trigonometric ratios for each of the triangles were equal.
- The value of the primary trigonometric ratios can change depending on the value of the reference angle.
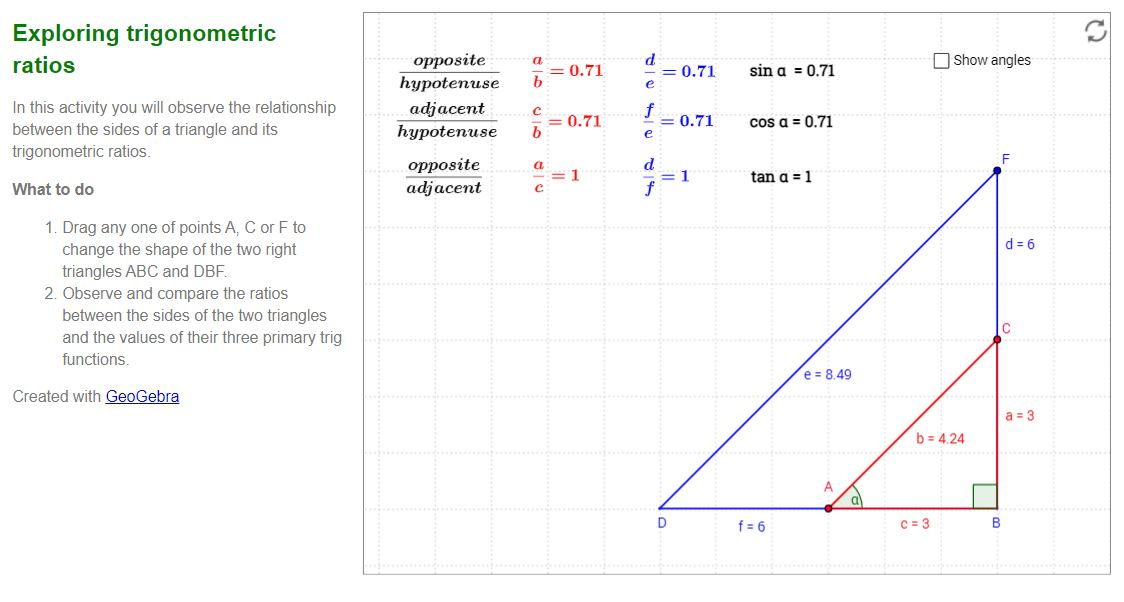
Investigating angles and primary trig ratios
Use the graphing app to explore the following:
- Choose an angle measure you want to explore (for example: 20°, 30°, 40°, and so on). You can try other values as you deem fit.
- Change the size of the triangle (note that the triangles are similar because the angles are the same: AA~).
- Move the triangle around.
- Observe the different ratios of the sides. Does it matter what size the triangle is, where the triangle is, or what the angle is?
What did you discover?
Based on your investigation, you may have discovered the following:
- For any given reference angle, the primary trigonometric ratios remain the same, regardless of the size of the triangle. For example, for a reference angle of , , , and . This means that the primary trigonometric ratios do not change for a given reference angle even if the size of the triangle changes.
- If you change the measure of the reference angle, the primary trigonometric ratios take on different values.
- The primary trigonometric ratios only apply to right triangles, otherwise we must use the ideas of similar and congruent triangles.
Keep these points in mind as you continue through the course. You’ll need them!
Join the discussion
Write out the steps you would take to determine if two triangles are similar. Be clear with your steps based on what you have learned so far focusing on using trigonometric ratios.
Using a scientific calculator: finding trig ratios
Calculators vary, so it is very important to figure out how your own calculator works. To begin, you may need to activate the degree mode. If you notice a [DEG] key, press it. If not, and you notice a [MODE] key, press that and then select the degree mode. Many of the simpler scientific calculators do not require this step.
Finding a ratio when you know the angle
Calculate the value for . Is your answer close to ? If not, try again or check the instructions for your calculator until you get the correct answer. For many calculators, you must input the degree of the angle before pressing the “sin” button.

Portfolio
Use your calculator to evaluate the following trigonometric ratios.

Mathematician Katherine Johnson
Imagine if we did not have a programmable calculator to assist us with these complicated equations.
Did you know that during a NASA mission in 1962, mathematician Katherine Johnson would run the same numbers and equations that were programmed into a computer to control the trajectory by hand? Johnson would only use a desktop calculating machine to ensure that the numbers matched the programmable numbers in the computer. Imagine if we had to check all our calculations!
Using a scientific calculator: finding angles
To find the measure of an angle given one of the trigonometric ratios, you may use the [INV] key, followed by the [SIN], [COS], or [TAN] key, or a key labelled [SIN−1], [COS−1], or [TAN−1].
NOTE: Angles are also represented by Greek symbols, such as θ (“theta”).
Finding an angle when you know the ratio
Calculate θ if cos θ=0.5.
Is your answer 60°? If not, try again or check the instructions for your calculator until you get the correct answer.
Portfolio
Ready for some more?
Use your calculator to evaluate the angle when the trigonometric ratio is given. (Round your answers to the nearest degree.)
Finding unknown sides and unknown angles
The trigonometric ratios are useful for solving problems where there is not enough information available to use the Pythagorean theorem, or even similar and congruent triangles. Side lengths and angle measures can be quickly calculated using the trigonometric ratios, with very little information.
Explore this!
The Pythagorean theorem
Explore the following video to learn more about the Pythagorean theorem.
Join the discussion
Summarize the idea of Pythagorean theorem from the video above. Why is Pythagorean theorem so important to understand when exploring triangles?
Notebook
You can use your notebook to answer the next series of questions.
Example 1
For each of the following examples, record your solutions in your notebook. When you’re finished, press Suggested Answer to check the solution.
Solve for the indicated side length.

Example 2
Solve for the indicated side length.

Example 3
Solve for the indicated side length.

Example 4
Solve for the indicated side length.

Example 5
Solve for the indicated side length and unknown angle.

Example 6
Solve for the indicated side length and unknown angle..

Notebook
Now that you’ve had some practice solving for unknown sides and angles, let’s attempt some questions where you can apply your algebraic skills. In your notebook, solve the following problems. You may need to draw a sketch first. When you’re finished, press Suggested Answer to compare your answers.
A ladder that is 5 m long is leaning against a wall, touching it 4 m above the ground.
- What angle is formed where the ladder meets the ground?
- What angle is formed where the ladder meets the wall?
- What is the distance from the base of the wall to the bottom of the ladder?
- At a point that is 20 m from a flagpole, the angle of elevation to the top of the flagpole is 54°.
- How high is the flagpole?
For safety reasons, the angle at which a ladder meets the ground should be between 65° and 80°. A ladder that is 5 m long is positioned so that it reaches the top floor window of a house.
- If the base of the ladder is 1.5 m from the house, is the ladder safe?
- Explain your answer.
Summary
Well done! You’ve successfully completed this learning activity.
In this learning activity, you:
- defined the formulas for the primary trigonometric ratios in terms of the sides of a right triangle
- solved for the unknown sides and angles in right triangles, using the primary trigonometric ratios
In addition, you should now have a strong understanding of the following concepts:
- Given a specific reference angle, the ratio of sides between similar triangles should remain the same.
- “SOH-CAH-TOA” is a simple way to recall the sides involved for the Primary Trigonometric Ratios.
- Using the inverse trigonometric features on your calculator will allow you to solve for an angle in a right triangle when two side lengths are given.
- The Primary Trigonometric Ratios apply to right triangles only. That is, there must be a 90° angle.
Revisit any areas where you need to strengthen your understanding.