Learning activity 1.7: Solving quadratics using the quadratic formula

In this learning activity, we are going to learn about the quadratic formula. The reason for learning this formula is that it is very helpful for solving quadratic equations that are difficult or impossible to factor. The quadratic formula can be used to solve any quadratic equation of the form $a x^{2} + b x + c = 0.$

Challenge

In the last activity you learned that one way you can solve quadratic problems is to factor.

Solve the following by factoring: $y = {2 x}^{2} + 4 x - 3$

$0 = {2 x}^{2} + 4 x - 3$

Determine two numbers that multiply to $- 6$ and add to $4$ .

Notice that there are no numbers that satisfy the criteria. In this case, the equation is not factorable.

If an equation is not factorable, we must use the formula to solve quadratic problems.

Explore this!

Let us explore the detailed steps used for solving quadratic equations in the following video.

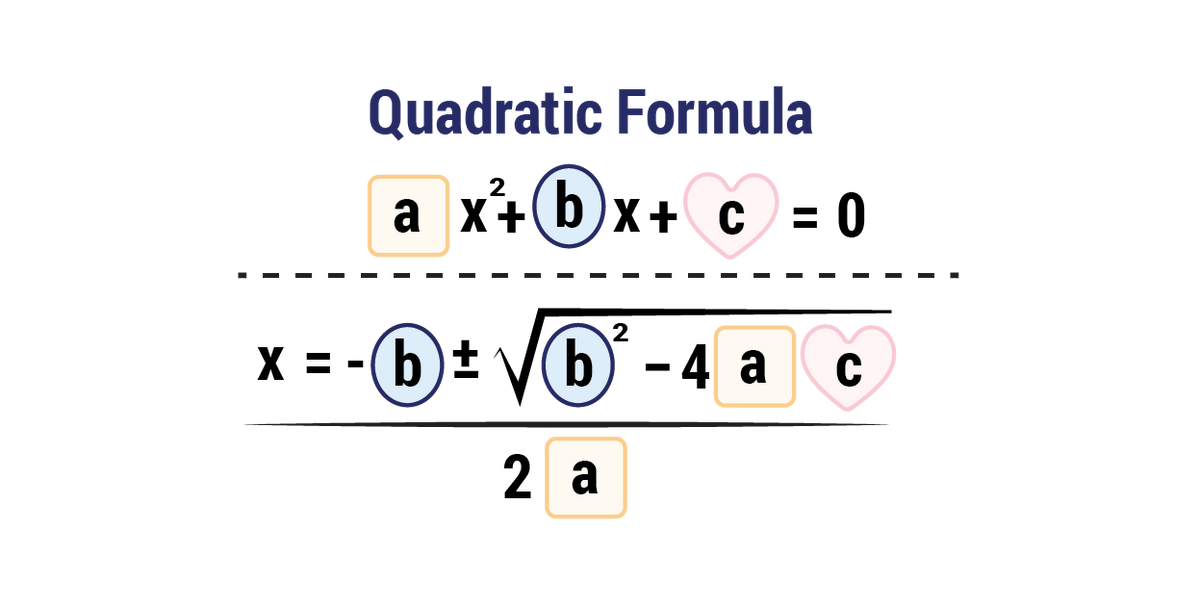
The quadratic formula:

We have learnt that any quadratic equation in standard form $a x^{2} + b x + c = 0$ , can be solved for $x$ by using the quadratic formula to find the roots. This is the formula:

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

The formal proof for the quadratic formula will be explained later in the course.

For the purpose of this activity, let’s confirm that the quadratic formula is just a different way of writing the standard form of a quadratic, $a x^{2} + b x + c = 0$

Explore this!

Explore the following video on the quadratic formula and its standard form variation.

The quadratic formula

When it is not possible to factor an equation, you must use the quadratic formula.

A crowd of people walking through a city street on a wet autumn day.

In the year 2017, a census counted a Canadian city’s population as 350,000 people. The population growth of the city is represented by the quadratic relation $P = 2 t^{2} + 11 t + 350$ , where $P$ is the population in thousands and $t$ is the time in years beginning in the year 2018. When will the population of the city reach 400,000?

Solve using standard form

Since the population $P$ is in thousands, then 400,000 is represented by $P = 400$ .

To find the time when the population is 400,000, substitute $P = 400$ into the equation and solve for $t$ :

Step 1: Get equation into standard form and equation equal to zero.

Sometimes you will have to substitute a value for the independent variable (Population in this case) and then rearrange.

$400 = 2 t^{2} + 11 t + 350$

$2 t^{2} + 11 t - 50 = 0$

Step 2: Determine the a, b, and c values.

Notice how the given equation corresponds with $a x^{2} + b x + c = 0$

$a = 2$ , $b = 11$ , and $c = - 50$

Step 3: Substitute the values into the quadratic formula and solve.

Note: There will be two options or “roots” at the end, one where you add the square rooted number and one where you subtract it.

In this step you are solving for the roots of the quadratic.

$t = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

$t = \frac{- (11) \pm \sqrt{{(11)}^{2} -4 (2) (-50)}}{2 (2)}$

$t = \frac{- 11 \pm \sqrt{121 + 400}}{4}$

$t = \frac{- 11 \pm \sqrt{521}}{4}$

$t = \frac{- 11 + \sqrt{521}}{4} or$ $t = \frac{-11 - \sqrt{521}}{4}$

$t ≅ 3 or t ≅ - 8.5$

Step 4: For word problems, use the intercepts to answer the question.

Time cannot be a negative number, so the only solution is $t = 3$ years.

Since the years begin at 2018, add $2018 + 3 = 2021$

Therefore, the population of the city will reach 400,000 in 2021.

In the last learning activity, you calculated the $x$ -intercepts for a situation where a person was throwing horseshoes.

Let’s review that solution beginning with the original equation given and ended with the $x$ -intercepts.

$h = - \frac{1}{50} (3 x^{2} - 37 x - 86)$

$0 = - \frac{1}{50} (3 x^{2} - 37 x - 86)$

$0 = - \frac{1}{50} (3 x - 43) (x + 2)$

$x = \frac{43}{3}$ or $x = - 2$

Solve using the quadratic formula

Now let’s examine if we would get the same result using the quadratic formula for the equation.

$h = - \frac{1}{50} (3 x^{2} - 37 x - 86)$

Step 1: Get equation into standard form and set equal to zero.

Sometimes you will have to substitute a value for the independent variable (height in this case) and then solve.

$0 = - \frac{1}{50} (3 x^{2} - 37 x - 86)$

Step 2: Identify the a, b, and c values

You are looking for $a$ , $b$ , and $c$ values from $a x^{2} + b x + c = 0$ based on the given equation.

This can be done after you have common factored.

You will get the same final result if you do or don’t common factor.

$a = 3$ $b = - 37$ $c = - 86$

Note that you could have expanded first and got $a = \frac{- 3}{50}$ $b = \frac{37}{50}$ $c = \frac{43}{25}$ but the $a,$ $b$ , and $c$ values will be easier to work with if we use the ones with the equation having been common factored.

Step 3: Substitute the values into the quadratic formula and solve

There will be two options at the end, one where you add the square rooted number and one where you subtract it

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

$x = \frac{- (- 37) \pm \sqrt{{(- 37)}^{2} - 4 (3) (- 86)}}{2 (3)}$

$x = \frac{37 \pm \sqrt{1,369 + 1,032}}{6}$

$x = \frac{37 \pm \sqrt{2,401}}{6}$

$x = \frac{37 + \sqrt{2,401}}{6}$ or $x = \frac{37 - \sqrt{2,401}}{6}$

$x = \frac{37 + 49}{6} or x = \frac{37 - 49}{6}$

$x = \frac{86}{6} or x = \frac{- 12}{6}$

$x = \frac{43}{3} or x = - 2$

Examples:

You recall that the roots of an equation are the value of $x$ when $y = 0$ . Use the quadratic formula to determine the roots of $2 x^{2} + 8 x - 1 = 0$ to one decimal place.

Follow the steps and check your work as you go.

$a = 2$

$b = 8$

$c = - 1$

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

$x = \frac{- (8) \pm \sqrt{{(8)}^{2} - 4 (2) (- 1)}}{2 (2)}$

$x = \frac{- 8 \pm \sqrt{64 + 8}}{4}$

$x = \frac{- 8 \pm \sqrt{72}}{4}$

$x = \frac{- 8 + \sqrt{72}}{4}$ $o r$ $x = \frac{- 8 - \sqrt{72}}{4}$

$x = \frac{- 8 + 8.5}{4} or x = \frac{- 8 - 8.5}{4}$

Therefore, $x = 0.1$ or $x = - 4.1$

Notice that the quadratic formula is not as easy, or as fast, as the factoring methods you have already learned, however, not all equations can be factored.

When a quadratic equation cannot be factored, the quadratic formula can be used to determine the $x$ -intercepts, or zeros, of the related graph.

As you’ve learned, the solutions to a quadratic equation represent the $x$ -intercepts of the graph of the corresponding relation.

The following is the graph of the quadratic relation $y = (3 x - 4) (2 x + 1) - 9$

Notebook

In your notebook, attempt the following questions on your own first. Round your answers to one decimal place.

When you’re finished, compare your answers with the suggested ones.

The zeros appear to be approximately -1.1 and 1.9, which is where the parabola crosses the $x$ -axis.

To solve, let $y = 0$ :

$0 = (3 x - 4) (2 x + 1) - 9$

$0 = 6 x^{2} + 3 x - 8 x - 4 - 9$

$0 = 6 x^{2} - 5 x - 13$

From the equation, $a = 6$ , $b = - 5$ , and $c = - 13$

Substitute these values into the quadratic formula:

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

$x = \frac{- (- 5) \pm \sqrt{{(- 5)}^{2} - 4 (6) (- 13)}}{2 (6)}$

$x = \frac{5 \pm \sqrt{25 + 312}}{12}$

$x = \frac{5 \pm \sqrt{337}}{12}$

$x = \frac{5 + \sqrt{337}}{12} or x = \frac{5 - \sqrt{337}}{12}$

$x \approx 1.95 or x \approx - 1.11$

The discriminant

In the quadratic formula, the expression underneath the square root sign is called the discriminant of the quadratic equation.

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

We can use the discriminant to determine if the graph of quadratic relation will have 0, 1, or 2 real roots ( $x$ -intercepts). The roots are real numbers if, and only if, the discriminant is non-negative.

At this point, you need to identify what is, or is not, a real number. You may have learned about real numbers in other mathematics courses. A real number is any number that can be written as either a fraction or non-terminating, non-repeating decimal.

Examples of real numbers:

$2$ , $- 9$ , $\frac{4}{3}$ , $8.21211211121111$ ..., $9.6$ , $\sqrt{3}$ .

Examples of numbers that are not real:

$\sqrt{- 3}$ , $\sqrt{- 4}$ , $5 + \sqrt{- 7}$ .

These are called complex numbers because they contain the square root of a negative number.

Explore this!

Let us explore the following video to better understand the nature of roots.

Let us now examine the following examples to understand how we can apply discriminant method to find the nature of roots of a quadratic equation.

Example 1

Consider the following quadratic equation: $y = x^{2} - 2 x + 3 .$

Use the graph to answer the following questions on your own. When you’re finished, compare your answers with the suggested ones.

From the graph, you can identify that this parabola does not intersect the $x$ -axis, so it does not have any $x$ -intercepts.

Let $y = 0$ to solve for the roots:

$0 = x^{2} - 2 x + 3$

Substitute $a = 1$ , $b = - 2$ , and $c = 3$ into the quadratic formula:

$x = \frac{- (- 2) \pm \sqrt{(- 2)^{2} - 4 (1) (3)}}{2 (1)}$

$x = \frac{2 \pm \sqrt{4 - 12}}{2}$

$x = \frac{2 \pm \sqrt{- 8}}{2}$

The roots are $x = \frac{2 + \sqrt{- 8}}{2}$ or $x = \frac{2 - \sqrt{- 8}}{2}$ .

Since $\sqrt{- 8}$ is not a real number, there are no real roots.

Since $\sqrt{- 8}$ is not a real number, there are no real roots and the graph does not have any $x$ -intercepts. Therefore, there are two complex roots but no $x$ -intercepts.

When the discriminant (the value under the radical sign) is negative, the roots are not real and so there are no $x$ -intercepts. Therefore, the part of the formula under the radical sign, $b^{2} - 4 a c$ , does indeed give you information about the absence of $x$ -intercepts of the graph.

Example 2

Consider the following quadratic equation: $y = x^{2} - 6 x + 9 .$

Use the graph to answer the following questions on your own. When you’re finished, compare your answers with the suggested ones.

From the graph, you can identify that this parabola intersects the $x$ -axis at $x = 3$ and so it has only one $x$ -intercept.

Let $y = 0$ to solve for the roots:

$0 = x^{2} - 6 x + 9$

Substitute $a = 1$ , $b = - 6$ , and $c = 9$ into the quadratic equation:

$x = \frac{- (- 6) \pm \sqrt{{(- 6)}^{2} - 4 (1) (9)}}{2 (1)}$

$x = \frac{6 \pm \sqrt{{36 - 36}^{}}}{2}$

$x = \frac{6 + 0}{2}$

$x = \frac{6}{2}$

$x = 3$

There is only one root, $x = 3$ .

There is only one root, $x = 3$ and there is only one $x$ -intercept of the graph.

When the discriminant is $0$ , the equation has only one real root and the graph has one $x$ -intercept.

Note: The root $x = 3$ is sometimes called a double root. The equation $x^{2} - 6 x + 9 = 0$ is a perfect square trinomial and can be factored as a binomial squared $(x - 3)^{2} = 0$ .

The solution has two equal binomials that produce the same root, as follows.

$(x - 3) (x - 3) = 0$

Either $x = 3$ or $x = 3$ .

$3$ appears twice, hence the name “double root.”

Example 3

Consider the following quadratic equation: $y = 3 x^{2} - 6 x - 1 .$

Notebook

Using your notebook, try the following questions on your own. When you’re finished, compare your answers with the suggested ones.

Determine the number of $x$ -intercepts from the graph.

From the graph, you can identify that this parabola intersects the $x$ -axis in two places and so it has two $x$ -intercepts.

Use the quadratic formula to determine the roots of the equation.

Let $y = 0$ to solve for the roots:

$3 x^{2} - 6 x - 1 = 0$

Substitute $a = 3$ , $b = - 6$ , and $c = - 1$ into the quadratic formula:

$x = \frac{- (- 6) \pm \sqrt{{(- 6)}^{2} - 4 (3) (- 1)})}{2 (3)}$

$x = \frac{6 \pm \sqrt{48}}{6}$

$x = \frac{6 + \sqrt{48}}{6}$ or $x = \frac{6 - \sqrt{48}}{6}$

$x = 2.15$ or $x = - 0.15$

Therefore, there are two real roots.

How does the number of roots relate to the number of $x$ -intercepts?

There are two real roots and there are two $x$ -intercepts.

Which part of the quadratic formula gives information about the number of $x$ -intercepts and what does it tell us in this case?

In the quadratic formula, the discriminant is positive and so produces two real roots. Since the roots are real, they are the $x$ -intercepts.

Example 4

This exercise demonstrates how to use the discriminant to find information about the roots and the $x$ -intercepts of a quadratic relation.

For each quadratic relation, determine the nature of the roots and the number of $x$ -intercepts of the corresponding graph.

Substitute $a = - 1$ , $b = 2$ , and $c = - 5$ into the discriminant:

$b^{2} - 4 a c$

$= 2^{2} - 4 (- 1) (- 5)$

$= 4 - 20$

$= - 16$

This number is negative.

Since $b^{2} - 4 a c < 0$ , there are no real roots and therefore the graph does not have $x$ -intercepts.

Substitute $a = 3$ , $b = 4$ , and $c = - 1$ into the discriminant:

$b^{2} - 4 a c$

$= 4^{2} - 4 (3) (- 1)$

$= 16 + 12$

$= 28$

This number is positive.

Since $b^{2} - 4 a c > 0$ , there are two real roots and the graph has two $x$ -intercepts.

Substitute $a = 4$ , $b = 12$ , and $c = 9$ into the discriminant:

$b^{2} - 4 a c = 12^{2} - 4 (4) (9)$

$= 144 - 144$

$= 0$

Since $b^{2} - 4 a c = 0$ , there is one (double) real root and therefore the graph has one $x$ -intercept.

Quadratic formula review

The roots of a quadratic equation in the form $a x^{2} + b x + c = 0$ can often be found by factoring using methods such as common factoring, x-trick, decomposition, or sum/product rule. Sometimes, however, it is not possible to use any of these methods. A more sophisticated approach is needed, like the quadratic formula!

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

Some key points

To use the quadratic formula, the quadratic equation must be written in a standard form.
All quadratic equations of the form $a x^{2} + b x + c = 0$ can be solved using the quadratic formula.
The quadratic formula is derived by completing the square for $a x^{2} + b x + c = 0$ and solving for x. It is a direct way of calculating roots without graphing or algebraic manipulation.
The quadratic formula sometimes leads to a negative number under the square root sign. When this happens, the calculation cannot be completed using ordinary (real) numbers. In this case, the relation has no real roots.

Quadratic formula and the discriminant

The portion of the quadratic formula under the square root sign provides a means to determine the nature and number of roots. This is portion is called the discriminant $(b^{2} - 4 a c)$

If …	…then the quadratic function has…
$b^{2} - 4 a c > 0$	Two distinct real roots
$b^{2} - 4 a c < 0$	No real roots
$b^{2} - 4 a c = 0$	One real root

Self-check

As a self-directed learner, you will be reflecting on your learning process and checking your understanding in order plan for success. Make a note of your understanding of the success criteria from today’s activity.

Rate your understanding on a scale of five to one.

Five means “I have a thorough understanding.” One means “I am confused.”

Are you able to

Statement	1	2	3	4	5
Solve quadratic problems by using the quadratic formula
Determine the number of $x$ -intercepts by using the discriminant

Portfolio

Math journal

At the end of the course, you will fine-tune 8 entries (two from each unit) from your math journal and submit them as your “Culminating Assessment - Math Journal.” (Opens in new window)

In this activity you learned how to solve quadratic problems by using the quadratic formula. Think about when you can use it, the steps you take to complete it, how easy you find it and why.

Add this method to solve quadratic relations into your math journal along with the situations when you use it. Your summary may resemble this:

Solving by using the quadratic formula

What does it mean to solve a quadratic relation?	Why must you set the equation to zero in order to solve a quadratic?	Explanation of steps	Example	How do the zeros relate to a graph? Include a graph of your example using a graphing app of your choice.	When can you use this method?

Create a summary in your math journal about the discriminant. Check your summary with the suggested answers. You summary can be in a chart format, flow chart, mind map, etc.

Discriminant	Nature of roots	Number of $x$ -intercepts	Graph
$b^{2} - 4 a c > 0$ (positive)
$b^{2} - 4 a c < 0$ (negative)
$b^{2} - 4 a c = 0$

Once you feel comfortable with the success criteria, try some questions to assess your progress.

Examples:

Solve the following using the quadratic formula. Round to one decimal place when necessary.

When you’re finished, compare your answers with the suggested ones.

x = 1.3

x = 0.2

$x = 2$ or $x = 2.5$

Making connections:

You have learned that the quadratic formula can be used to find the roots of all quadratic equations, even those that can be factored. Since it is often faster to find the roots by factoring than by using the quadratic formula, factor where possible and use the quadratic formula only when the equation cannot be factored.

Let’s examine three more equations. The next exercise will illustrate you that a quadratic equation can be factored when the discriminant equals a perfect square number (such as 1, 4, 9, 16, 25, and so on).

Notebook

In your notebook, solve each equation using the stated method.

Example 1:

Solve $6 x^{2} - 5 x - 4 = 0$ using the quadratic formula.

Substitute $a = 6$ , $b = - 5$ , and $c = - 4$ in the quadratic formula:

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

$x = \frac{- (- 5) \pm \sqrt{{(- 5)}^{2} - 4 (6) (- 4)}}{2 (6)}$

$x = \frac{5 \pm \sqrt{25 + 96}}{12}$

$x = \frac{5 \pm \sqrt{121}}{12}$

$x = \frac{5 \pm 11}{12}$

$x = \frac{5 + 11}{12}$ or $x = \frac{5 - 11}{12}$

$x = \frac{16}{12}$ or $x = \frac{- 6}{12}$

$x = \frac{4}{3}$ or $x = - \frac{1}{2}$

The roots are $x = \frac{4}{3}$ and $x = - \frac{1}{2}$

Solve this one again using factoring.

$0 = 6^{2} - 5 x - 40 = (3 x - 4) (2 x + 1)$

Either $3 x - 4 = 0$ or $2 x + 1 = 0$ .

Therefore, $x = \frac{4}{3}$ or $x = - \frac{1}{2}$ .

The roots are $x = \frac{4}{3}$ or $x = - \frac{1}{2}$ .

Example 2:

Solve $4 x^{2} = 7 x + 2$ using the quadratic formula.

Rearrange the formula:

$0 = 4 x^{2} - 7 x - 2$

Substitute $a = 4$ , $b = - 7$ ,and $c = - 2$ in the quadratic formula:

$x = \frac{- (- 7) \pm \sqrt{{(- 7)}^{2} - 4 (4) (- 2)}}{2 (4)}$ $x = \frac{7 \pm \sqrt{49 + 32}}{8}$

$x = \frac{7 \pm \sqrt{81}}{8}$

$x = \frac{7 + 9}{8}$

$x = \frac{16}{8}$

$x = 2$

$x = \frac{7 - 9}{8}$

$x = - \frac{2}{8}$

$x = - \frac{1}{4}$

Therefore, the roots are $x = 2$ or $x = - \frac{1}{4}$ .

Solve this one again using factoring.

Rearrange the formula:

$0 = {4 x}^{2} - 7 x - 20 = (x - 2) (4 x + 1)$

Either $x - 2 = 0$ or $4 x + 1 = 0$ .

Therefore, $x = 2$ or $x = - \frac{1}{4}$ .

The roots are $x = 2$ or $x = - \frac{1}{4}$ .

Example 3:

Solve $2 x (4 x + 5) = - 3$ using the quadratic formula.

Rearrange the formula:

$0 = {8 x}^{2} + 10 x + 3$

Substitute $a = 8$ , $b = 10$ , and $c = 3$ in the quadratic formula:

$x = \frac{- (10) \pm \sqrt{{(10)}^{2} - 4 (8) (3)}}{2 (8)}$ $x = \frac{- 10 \pm \sqrt{100 - 96}}{16}$ $x = \frac{- 10 \pm \sqrt{4}}{16}$ $x = \frac{- 10 + 2}{16}$

$x$ = $\frac{- 10 + 2}{16}$

$x$ =- $\frac{8}{16}$

$x$ =- $\frac{1}{2}$

$x$ = $\frac{- 10 - 2}{16}$

$x = - \frac{12}{16}$

$x = - \frac{3}{4}$

The roots are $x = - \frac{1}{2}$ or $x = - \frac{3}{4}$

Solve this one again using factoring.

$0 = {8 x}^{2} + 10 x + 30 = (x + 3) (2 x + 1)$

Either $4 x + 3 = 0$ or $2 x + 1 = 0$

Therefore, $x = - \frac{1}{2}$ or $x = - \frac{3}{4}$ .

The roots are $x = - \frac{1}{2}$ or $x = - \frac{3}{4}$ .

Answer the following questions based on the equations from this exercise:

$6 x^{2} - 5 x - 4 = 0$
$4 x^{2} = 7 x + 2$
$2 x (4 x + 5) = - 3$

What are the values of the discriminant for each equation?

The value of the discriminant for $6 x^{2} - 5 x - 4 = 0$ is $121$ .
The value of the discriminant for $4 x^{2} = 7 x + 2$ is $81$ .
The value of the discriminant for $2 x (4 x + 5) = - 3$ is $4$ .

What is similar about these values?

They are all perfect squares.

What conclusion can you make about when the value of the discriminant is a perfect square?

A quadratic relation is factorable when the discriminant is a perfect square.

Assessment Opportunity Math - Journal submission

To prepare you for the culminating assessment, you have the opportunity to submit a journal entry from this unit to be assessed for feedback before the final culminating assessment. It will be assessed according to the culminating assessment rubric. You may choose to make any updates of suggestions and submit it for the culminating assessment at the end of the course. Make sure to refer to the culminating task requirements for clarification of expectations.

Culminating Assessment: Math Journal Rubric

Please explore the rubric below to ensure full understanding of the assessment guidelines. When you are ready, submit your assessment for feedback following the submission directions. Though you will not receive a grade for this submission, the rubric is being included to remind you of the feedback that the teacher will be using to assess your final math journal submissions towards the end of the course.

You may receive the following forms of feedback: 

Your teacher may highlight the phrases on the rubric that best describe your assignment to show you how you have done.
Your teacher may also provide you with detailed comments about the strengths of your assignment, the areas of the assignment that need improvement, and the steps you should take before submitting another assignment like this one.

Pay careful attention to the following rubric. Your teacher will use it to assess your work. You should refer to it too, so you’ll know exactly what your finished assignment should appear like.

Knowledge & Understanding

Success Criteria:

knowledge of relevant and appropriate skills and procedures
knowledge of relevant and appropriate facts and terms
understanding of the meaning of the mathematical content

Level 4	Level 3	Level 2	Level 1
With a high degree of effectiveness	With considerable effectiveness	With some effectiveness	With limited effectiveness

Thinking

Success Criteria:

logical interpretation of problem
evidence of modelling the problem, drawing conclusions, or justifying reasoning

Level 4	Level 3	Level 2	Level 1
With a high degree of effectiveness	With considerable effectiveness	With some effectiveness	With limited effectiveness

Communication

Success Criteria:

math vocabulary used accurately
math notation and symbols used appropriately
algebraic solutions, graphs, charts, diagrams organized and clearly written
mathematical thinking expressed clearly reflection on mathematical thinking expressed clearly

Level 4	Level 3	Level 2	Level 1
With a high degree of effectiveness	With considerable effectiveness	With some effectiveness	With limited effectiveness

Application

Success Criteria:

relevant and appropriate selection of facts, skills, procedures
relevant and appropriate connections made between math concepts
relevant and appropriate connections made between math and the world outside the classroom

Level 4	Level 3	Level 2	Level 1
With a high degree of effectiveness	With considerable effectiveness	With some effectiveness	With limited effectiveness

Challenge

Explore this!

The quadratic formula:

Explore this!

The quadratic formula

Solve using standard form

Step 1: Get equation into standard form and equation equal to zero.

Step 2: Determine the a, b, and c values.

Step 3: Substitute the values into the quadratic formula and solve.

Step 4: For word problems, use the intercepts to answer the question.

Solve using the quadratic formula

Step 1: Get equation into standard form and set equal to zero.

Step 2: Identify the a, b, and c values

Step 3: Substitute the values into the quadratic formula and solve

Examples:

Step 1: Identify the a , b , and c values.

Step 2: Substitute these values into the quadratic formula and solve.

Notebook

Use the graph to estimate the zeros or x -intercepts.

Use the quadratic formula to confirm your answers from part a).

The discriminant

Explore this!

Example 1

How many x -intercepts are there?

What are the roots of the equation? (Use the quadratic formula.)

How does the number of roots relate to the number of x -intercepts?

Which part of the quadratic formula gives information about the number of x -intercepts and what does it tell you in this case?

Example 2

How many x -intercepts are there?

What are the roots of the equation? (Use the quadratic formula.)

How does the number of roots relate to the number of x -intercepts?

Which part of the quadratic formula gives information about the number of x -intercepts and what does it tell us in this case?

Example 3

Notebook

Example 4

y = − x 2 + 2 x - 5

y = 3 x 2 + 4 x - 1

y = 4 x 2 + 12 x + 9

Quadratic formula review

Some key points

Quadratic formula and the discriminant

Self-check

Are you able to

Portfolio

Solving by using the quadratic formula

Examples:

4 x 2 - 6 x + 1 = 0

- 2 x + 7 x - 1 = 3

Making connections:

Notebook

Example 1:

Example 2:

Example 3:

Assessment Opportunity Math - Journal submission

Culminating Assessment: Math Journal Rubric

Knowledge & Understanding

Thinking

Communication

Application