Learning activity 1.4: Trigonometry and right angles

Introduction

Wooden frame of a house under construction

What is trigonometry? The word comes from two Greek words meaning “triangle” and “measure.” Trigonometry is a branch of mathematics that involves the measurement of sides and angles in triangles.

Trigonometry can be very useful in building and design. It is especially important in architecture and structural design, where it plays a role in the strength and stability of houses and other buildings. It is also useful in surveying, navigation, and other disciplines.

Have you ever noticed how many beams and wall supports are on an angle when a house is being built? Have you noticed that stairs and roofs are all made of triangles? This is due in part to the sturdiness of triangles. Triangles are the strongest straight-line shapes. They are harder to bend or break than rectangular shapes.

This learning activity will introduce you to the methods and formulas for finding the sides and angles of right-angled triangles.

Before you begin, it is important that your calculator is in the correct mode and you know how to use its trigonometric features. Most scientific calculators have three modes:

Degrees (deg or D)
Radians (rad or R)
Gradians (grad or G)

In this course, we will be working in degrees. Take a moment to ensure your calculator is in degree mode. If you need assistance with this, ask your teacher or a classmate.

Your scientific calculator will have three buttons for the primary trigonometric ratios: sine, cosine, and tangent. You will use these when you are determining the side length ratios in a right triangle.

Try it!

Use your calculator to determine the following. Round your answers to four decimal places if necessary. You can compare your answers when the suggested answers after you have determined the values.

Solve:	Answer:
sin 30°	0.5
cos 65°	0.4226
tan 27°	0.5095

Near the sin, cos, and tan buttons on your calculator, you will find the inverse trigonometric functions: sin^-1, cos^-1, and tan^-1. These buttons are used when you are determining the measurement of an angle in a right triangle.

Try it!

Use your calculator to determine the following. Round your answers to the nearest degree. You can compare your answers when the answers after you have determined the values.

Solve:	Answer:
sin^-1 (0.9205)	67°
cos^-1 (0.9703)	14°
tan^-1 (1)	45°

Triangle basics

Trigonometry is a branch of mathematics that deals with the relationships between the sides and the angles of a triangle. Trigonometry allows us to use known information (the measures of some angles and side lengths) to determine the unknown angles and side lengths.

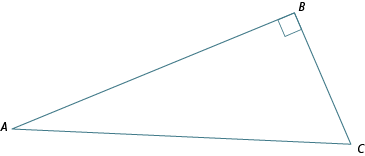
Trigonometry can be used for any kind of triangle, but we’ll start our study using a right-angled triangle like the one shown. Learn more about the key features by exploring each term before you move on.

Right angle

A right-angled triangle has one angle that is 90°. This kind of triangle is one of the most important and useful shapes in mathematics.

The right angle is indicated by a small square at the vertex.

Vertices

These are the corners of the triangle where the angles are located. A single corner is called a vertex.

The point at each vertex is labelled with a capital letter. In this triangle, the vertices are at points A, B, and C.

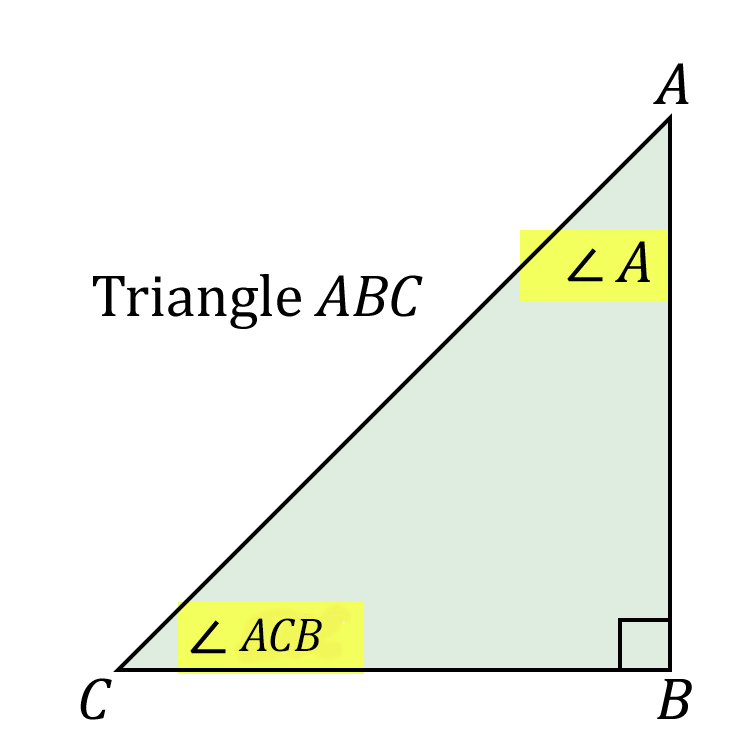
Triangle ABC, Angle highlighted (Angle A, Angle ACB)

Angles

An angle is the number of degrees between the two arms of a vertex.

An angle can be named by the letter of that vertex (i.e., ∠A). It can also be named by the letters that outline the angle, with the angle's vertex letter in the middle (i.e., ∠ACB).

Triangle ABC, sides are highlighted (Side AB, BC, AC)

Triangle sides

Triangle sides can be labelled in different ways. One way is to use the capital letters that appear at the ends of each line segment.

In this triangle, the three sides are AB, AC, and BC.

Triangle ABC, name highlighted. Triangle ABC

Triangle name

A triangle is named by listing its three vertices after a triangle symbol (Δ). So the name of this triangle is ΔABC.

You may be wondering why there are two different ways of labelling angles. Wouldn’t it be easier to simply use the letter that identifies the vertex?

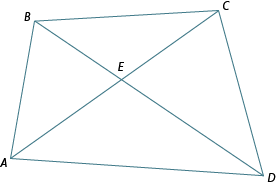
Kite shaped polygon. Vertices labelled A,B, C, D. A center point, E is labelled on the interior.

Consider the following polygon. If someone were to tell you $∠ E$ is 100°, which angle would they be referring to?

Because $∠ E$ is a point on the diagram where there are four angles, a more specific way of labelling each angle is required. In this situation, three letters are needed to identify the correct angle.

If someone were to tell you $∠ C E D$ is 100°, this would clear up the confusion.

Try it!

Study the following diagram, and answer the multiple-choice questions. If you answer any questions incorrectly, review the concepts previously mentioned before continuing the lesson.

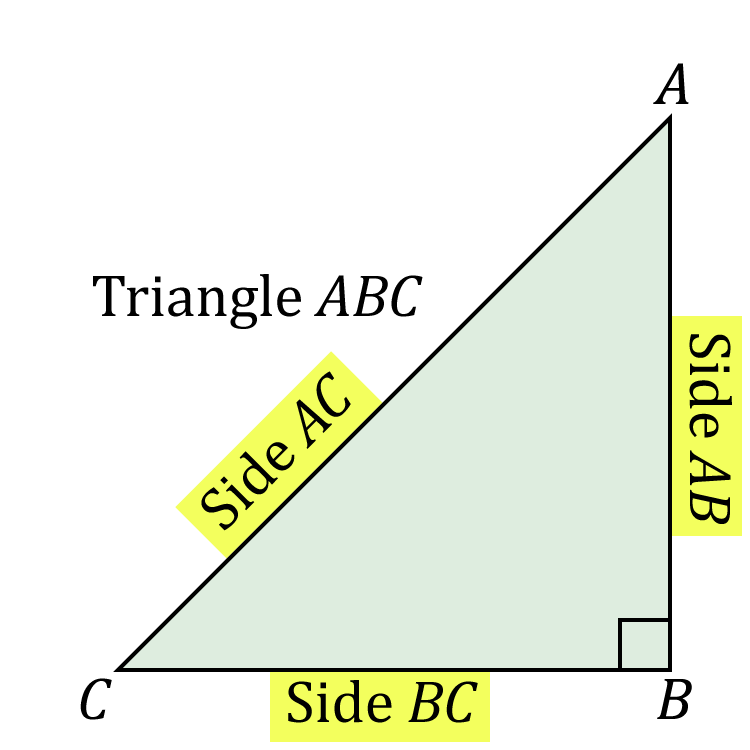
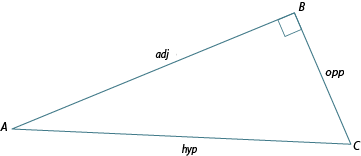
Naming the sides of a right-angled triangle

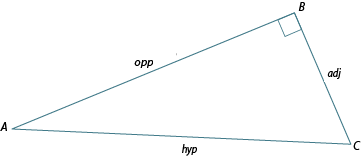
So far you have learned to use letters to label the sides of a triangle. However, sometimes in trigonometry we use more descriptive names.

You already know that the square at $∠ B$ represents a 90° angle. The side across from $∠ B$ , which is $A C$ , is called the hypotenuse of the triangle. The hypotenuse, "hyp" for short, is always the side across from the 90° angle in a right-angled triangle. It is always the longest side of the triangle.

Now let's name the other two sides. Their names will depend on which angle we are focusing on.

To do this, we must first choose one of the other two angles in the triangle. Let's choose $∠ A$ as the focus of our attention.

Using the diagram of the right-angled triangle, you will notice the side opposite $∠ A$ is $B C$ . We will call this the opposite side, or "opp" for short.

The last side in the triangle is called the adjacent side, "adj" for short, because it is beside $∠ A$ .

Notice that there are two sides next to $∠ A$ . They are called the adjacent side and the hypotenuse. We know the hypotenuse is always across from the 90° angle, so the other side next to $∠ A$ is the adjacent side.

When you label the sides of a right-angled triangle, always label the hypotenuse first, followed by the opposite side and then the adjacent side. This will avoid confusion.

Now all three of the sides in this triangle have names. Here is our labelled triangle, provided we are naming it in relation to angle $∠ A$ :

Right-angle triangle, side AB 'adj', side BC 'opp', side 'hyp'

Why does it matter?

At this point, you’re probably wondering why it’s important for us to focus our attention on one particular angle before we label the opposite and adjacent sides of the triangle.

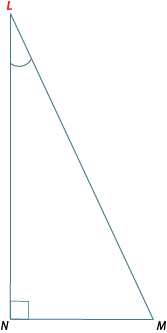
Let's consider what would happen if we chose $∠ C$ as the focus of our attention, instead of $∠ A$ .

The hypotenuse is always opposite the right-angle, so this label never changes.

But the opposite side to $∠ C$ is now $A B$ . Did you notice $A B$ was the adjacent side when we labelled the triangle in relation to $∠ A$ ?

The side adjacent to $∠ C$ is now $B C$ . Did you notice $B C$ was the opposite side on our previous diagram?

Right-angle triangle, side AB 'opp', side BC 'adj', side 'hyp'

The labels we apply to the opposite and adjacent sides of the triangle depend on the angle we are focusing our attention on. You will discover why this is important by the end of this learning activity.

Now it’s your turn.

Try it!

How would you label the triangle in relation to $∠ M$ ?

Triangle LMN. The bottom right vertice is 'M.' Angle N is a right-angle.

Match the descriptive labels in the right-hand column to the sides of the triangles shown on the left.

Here is the very same triangle. Now you'll consider how you would label the sides in relation to $∠ L$ .

Triangle LMN. The top vertice is 'L.' Angle N is a right-angle.

Match the descriptive labels in the right-hand column to the sides of the triangles shown on the left.

Therefore, to be able to label the opposite and adjacent sides of a triangle, we need to know which angle we’re focusing on.

Now that you’re comfortable with triangle basics, you’re ready to explore the primary trigonometric ratios.

The primary trigonometric ratios

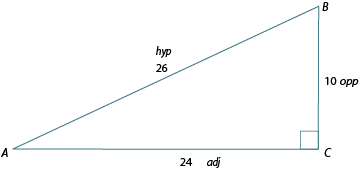
Let's examine $Δ A B C$ once again. There are three sides in this triangle – $A B$ , $A C$ , and $B C$ . How many ways can we choose two sides out of three?

The possibilities are $A B$ and $A C$ , $A B$ and $B C$ , or $A C$ and $B C$ . There are three ways to choose a pair of sides.

Now let's label the triangle descriptively in relation to $∠ A$ as we did earlier in this learning activity.

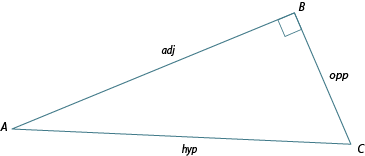
Triangle ABC. Side AB called 'adj', BC is 'opp, AC is 'hyp'

In $Δ A B C$ , there are three ways to choose a pair of sides: opposite and hypotenuse, adjacent and hypotenuse, or opposite and adjacent.

The three primary trigonometric ratios (often called “trig” ratios) are based on these three pairs of sides. Ratios are a comparison of two numbers. The ratio of thumbs to fingers on your right hand can be written as 1 to 4, 1:4, or $\frac{1}{4}$ . We will use fractions to represent the primary trigonometric ratios, which are shown in the table:

$\frac{o p p}{h y p} \frac{a d j}{h y p} \frac{o p p}{a d j}$

Sine, cosine, and tangent

The special names for the primary trig ratios are sine, cosine, and tangent. These names are abbreviated to three letters, just as the names of the sides in a right-angled triangle are. The three primary trigonometric ratios are:

$\sin = \frac{o p p}{h y p} \cos = \frac{a d j}{h y p} \tan = \frac{o p p}{a d j}$

These ratios will allow you to determine the size of the angles and sides in right-angled triangles when some of these values are not given or known.

Here is an acronym to help you learn the primary trigonometric ratios:

SOH CAH TOA

It is pronounced "soak-a-toe-a" and represents each of the three ratios.

SOH reminds you that Sin is Opp over Hyp: $\sin = \frac{o p p}{h y p}$

CAH reminds you that Cos is Adj over Hyp: $\cos = \frac{a d j}{h y p}$

TOA reminds you that Tan is Opp over Adj: $\tan = \frac{o p p}{a d j}$

Explore this!

In the following video, you will learn how to calculate the sine, cosine, and tangent ratios.

Starting at time 4:05, the narrator talks about three other trigonometric ratios, which we refer to as the “Secondary Trig Ratios”. Those three ratios are not covered in this course and can be disregarded.

Let’s consider an example.

Example

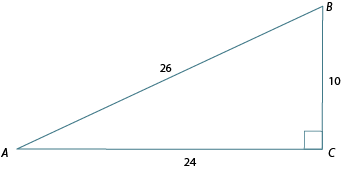
Use the definitions just learned to find the sine, cosine and tangent of $∠ A$ in the following triangle. Then, using your calculator, round your answers to four decimal places.

Triangle ABC. Side AB '26', BC '10', AC '24'. Angle C is a right angle.

First label the triangle in relation to $∠ A$ .

Triangle ABC. Side AB: hyp, 26. BC: opp, 10. AC: adj, 24. Angle C is a right angle.

Then calculate the ratios:

$\begin{array}{l} \sin A = \frac{o p p}{h y p} \\ = \frac{10}{26} \\ \approx 0.3846 \end{array}$

$\begin{array}{l} \cos A = \frac{a d j}{h y p} \\ = \frac{24}{26} \\ \approx 0.9231 \end{array}$

$\begin{array}{l} \tan A = \frac{o p p}{a d j} \\ = \frac{10}{24} \\ \approx 0.4167 \end{array}$

Notebook

Now it's your turn to try it in your notebook!

Using the same triangle in the previous example (shown here again), re-label the sides in relation to $∠ B$ , and then calculate the three primary trig ratios for $∠ B$ .

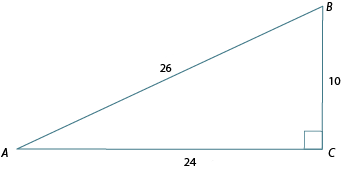
Triangle ABC. Side AB: hyp, 26. BC: adj, 10. AC: opp, 24. Angle C is a right angle.

Compare your answer to the "Suggested Answer" provided.

$\begin{array}{l} \sin B = \frac{o p p}{h y p} \\ = \frac{24}{26} \\ \approx 0.9231 \end{array}$

$\begin{array}{l} \cos B = \frac{a d j}{h y p} \\ = \frac{10}{26} \\ \approx 0.3846 \end{array}$

$\begin{array}{l} \tan B = \frac{o p p}{a d j} \\ = \frac{24}{10} \\ \approx 2.4 \end{array}$

Calculating sides and angles

Now that you’re familiar with the primary trig ratios, it’s time to tackle some problems. In this section of the learning activity, you’ll explore two types of problems:

calculating the length of a side
calculating the size of an angle

Later in the learning activity, you will discover how these calculations are important in real-world applications.

Calculating the length of a side

In this type of problem, there are two known measurements - an angle (other than the right angle) and a side. You will be asked to find a second side.

To determine the length of a side, follow these steps:

Label the sides of the triangle descriptively, in relation to the given angle.
Circle the given angle, the given side, and the side you are asked to find.
Use SOH CAH TOA to determine the primary trig ratio that includes the sides you have circled.
Write an equation using the primary trig ratio you determined in step 3.
Use a scientific calculator to solve the equation. Make sure your calculator is in degree mode.
Write a word answer stating your solution that includes units.

Let’s find out how to calculate the length of a side with the help of some examples.

Example 1: Calculating the length of a side

Calculate the length of side BC in the following triangle, accurate to one decimal place.

Triangle ABC. Angle A: 40 degrees. Side AB: 16.0 m.

Solution

Step 1

Label the triangle. Since we are given $∠ A = 40 °$ , we can label the rest of the triangle descriptively in relation to $∠ A$ . We will use $x$ to represent the unknown side.

Triangle ABC. Angle A: 40 degrees. Side AB: 16.0 m, hyp. AC: adj. BC: x, opp.

Step 2

Circle $∠ A$ , hyp, and opp.

Step 3

Choose a trig ratio based on the given side (hyp) and the one we wish to find (opp). We will choose the sine ratio as it's the one that includes the opposite side and the hypotenuse.

Step 4

Write the appropriate equation, substituting in the given information:

$\sin A = \frac{o p p}{h y p}$

$∴ \sin 40 ° = \frac{x}{16}$

$(multiply both sides of the equation by 16)$

$x = 16 (\sin 40 °)$

Step 5

Solve the equation using your scientific calculator. You will need to use the "sin" button, and make sure your calculator is in degree mode. On most calculators, you will press the "sin" button, type 40, and press the equals sign (=). Keep in mind that "sin 40°" is a number! It represents the ratio of the opposite side to the hypotenuse.

$x \approx 10.3$

Step 6

Write a word answer including units.

Therefore, side $B C$ is approximately 10.3 m long.

Example 2: Calculating the length of a side

Calculate the length of GH in the following triangle, accurate to one decimal place.

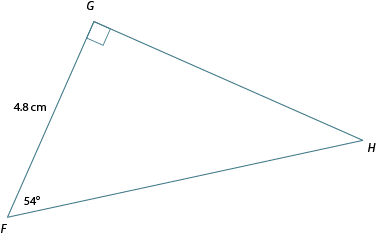
Triangle FGH. Angle F: 54 degrees. Side FG: 4.8 cm.

Solution

Step 1

Label the diagram in relation to $∠ F$ (the given angle). We will use $x$ to represent the unknown side.

Triangle FGH. Angle F: 54 degrees. Side FG: 4.8 cm, adj. GH: x, opp. FH: hyp.

Step 2

Circle $∠ F$ , adj, and opp.

Step 3

Choose a trig ratio based on the given side (adj), and the one we wish to find (opp). Since the tangent ratio is the one which includes the opposite and adjacent sides, we will choose the tangent ratio.

Step 4

Write the appropriate equation, substituting in the given information:

$\tan F = \frac{o p p}{a d j}$

$∴ \tan 54 ° = \frac{x}{4.8}$

$(multiply both sides of the equation by 4.8)$

$x = 4.8 (\tan 54 °)$

Step 5

Solve the equation using your scientific calculator. You will need to use the "tan" button, and make sure your calculator is in degree mode. Keep in mind that "tan 54°" is a number! It represents the ratio between the opposite and adjacent sides.

$x \approx 6.6$

Step 6

Write a word answer including units.

Therefore, side $G H$ is approximately 6.6 cm long.

Notebook

You can use your notebook to draw the triangles and answer the next series of questions. Keep in mind that you need to include units in your final answers.

Calculate the length of AB in the following triangle, accurate to one decimal place.

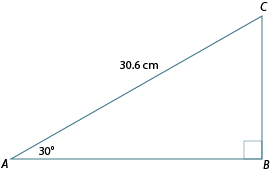
Triangle ABC. Angle A: 30 degrees. Side AC: hyp, 30.6 cm.

Label the diagram in relation to $∠ A$ .

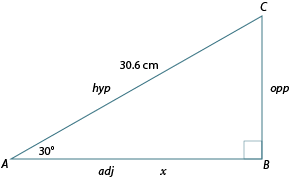
Triangle ABC. Angle A: 30 degrees. Side AC: hyp, 30.6 cm. CB: opp. AB: adj, x.

Since the cosine ratio is the one which includes the adjacent side and the hypotenuse, we will choose the cosine ratio.

$\cos 30^{°} = \frac{x}{30.6}$

$x = 30.6 (\cos 30^{°})$

$x = 26.5$

The length of $A B$ is approximately 26.5 cm.

What’s the extra step?

Sometimes solving the equation in step 4 is a bit more difficult. This happens when the unknown side (x) is in the denominator of the trig ratio. In this case, you need to perform an extra step, as the following example demonstrates.

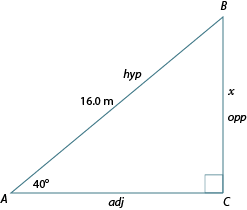
Example: Finding x when it's in the denominator of the trig ratio.

Calculate the length of side AC, accurate to the nearest mm.

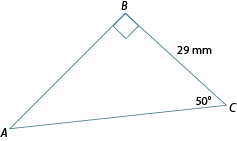
Triangle ABC. Angle C: 50 degrees. BC: 29mm. AB: opp.

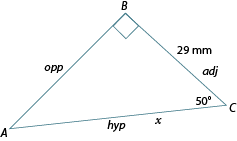
Triangle ABC. Angle C: 50 degrees. Side AC: hyp, x. BC: adj, 29mm. AB: opp.

Label the diagram in relation to $∠ C$ before you begin. Circle $∠ C$ , the given side (adj), and the side we wish to find (hyp), which will be the unknown side $(x)$ .

Which of the three primary trig ratios includes the adjacent side and the hypotenuse? It’s the cosine ratio!

Write the cosine equation and substitute in the given information.

$\cos C = \frac{a d j}{h y p}$

$\cos 50 ° = \frac{29}{x}$

$x (\cos 50 °) = 29 (multiply both sides of the equation by x)$

$x = \frac{29}{\cos 50 °} (divide both sides of the equation by \cos 50° to isolate x)$

$x \approx 45$

Therefore, side $A C$ is approximately 45 mm long.

Notebook

You can use your notebook to draw the triangles and answer the next series of questions. Keep in mind that you need to include units in your final answers.

Calculate the length of LM, accurate to one decimal place.

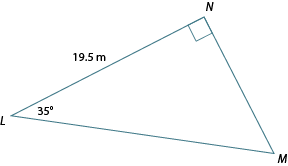
Triangle LMN. Angle L: 35 degrees. Side LN: 19.5m.

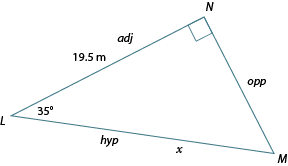
Triangle LMN. Angle L: 35 degrees. Side LN: adj, 19.5m. Side MN: opp. Side LM: hyp, x.

Label the triangle in relation to $∠ L$ and put an $x$ on side $L M$ .

$\cos (∠ L) = \frac{a d j}{h y p}$

$\cos (35^{°}) = \frac{19.5}{x}$

$x \cos (35^{°}) = 19.5$

$x = \frac{19.5}{\cos (35^{°})}$

$x = 23.8$

Therefore, side $L M$ is approximately 23.8 m long.

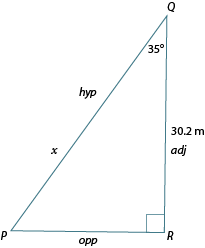
Calculate the length of PQ, accurate to one decimal place.

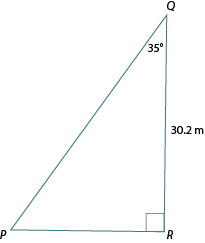
Triangle PQR. Angle Q: 35 degrees. Side QR: 30.2 m.

Label the triangle in relation to $∠ Q$ and put an $x$ on side $P Q$ .

$\cos (∠ Q) = \frac{a d j}{h y p}$

$\cos (35^{°}) = \frac{30.2}{x}$

$x \cos (35^{°}) = 30.2$

$x = \frac{30.2}{\cos (35^{°})}$

$x = 36.9$

Therefore, side $P Q$ is approximately 36.9 m long.

Triangle PQR. Angle Q: 35 degrees. Side QR: adj, 30.2m. Side PR: opp. Side PQ: hyp, x.

Calculating the size of an angle

To find the size of an angle in a right-angled triangle, you will use a method similar to the one you used for finding a side.

Follow these steps:

Label the sides of the triangle descriptively, based on the angle you wish to calculate.
Use SOH CAH TOA to determine the appropriate trig ratio based on the two known sides.
Solve the resulting equation using a scientific calculator (in degree mode).
Write a word answer stating your solution that includes units.

Let’s consider an example.

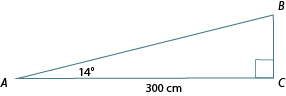
Example 1: Calculating the size of an angle

Calculate the size of $∠ A$ , to the nearest degree.

Triangle ABC. Angle A: ? degrees. Side AB: 23.6. BC: 13.5

Label the triangle in relation to $∠ A$ :

Triangle ABC. Angle A: ? degrees. Side AB: adj, 23.6. BC: opp, 13.5. AC: hyp

Which trig ratio includes the adjacent and opposite sides?

It's the tangent ratio!

$\begin{array}{l} \tan A = \frac{o p p}{a d j} \\ \tan A = \frac{13.5}{23.6} \end{array}$

Now we have a new problem. We wish to find $∠ A$ , not $\tan A$ .

Therefore, we must calculate the inverse of $\tan A$ , which is written $\tan^{- 1} (\frac{o p p}{a d j})$ .

To do this, we use the inverse (inv) or second function (2nd) button on our scientific calculator followed by pressing the tan button.

This is the calculation you will be performing.

$\begin{array}{l} ∠ A = \tan^{- 1} (\frac{13.5}{23.6}) \\ ∠ A = 30^{°} \end{array}$

Therefore, $∠ A$ is approximately 30°.

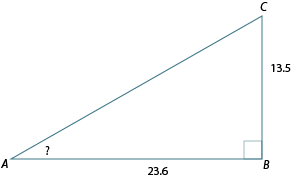
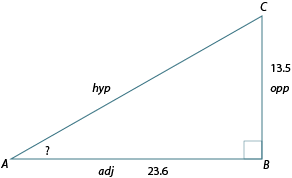
Example 2: Calculating the size of an angle

Calculate the size of $∠ P$ , to the nearest degree.

Triangle PQR. Angle P: ? degrees. Side PR: 8.0m. RQ: 2.0m

Our diagram, labelled in relation to $∠ P$ , will be like this:

Since the two known sides are the opposite and hypotenuse, we will use the sine ratio and then the inverse sine function on our scientific calculator.

The inverse sine of $A$ is written as $\sin^{- 1} (\frac{o p p}{h y p})$ .

$\begin{array}{l} \sin (∠ P) = \frac{o p p}{h y p} \\ \sin (∠ P) = \frac{2.0}{8.0} \\ ∠ P = \sin^{- 1} (\frac{2.0}{8.0}) \\ ∠ P = 14^{°} \end{array}$

Therefore, $∠ P$ is approximately 14°.

Notebook

You can use your notebook to draw the triangles and answer the next series of questions. Keep in mind to write the units for your answers.

Calculate the size of the unknown angle, to the nearest degree.

Triangle ABC. Angle C: ? Side AB: 15.7. BC: 21.8

$\begin{array}{l} ∠ C = \tan^{- 1} (\frac{15.7}{21.8}) \\ ∠ C = {35.76}^{°} \end{array}$

Therefore, $∠ C$ is approximately 36°.

Calculate the size of the unknown angle, to the nearest degree.

Triangle XYZ. Angle Z: ? Side XY: 9.8 cm. YZ: 12.5 cm

$\begin{array}{l} ∠ Z = \sin^{- 1} (\frac{9.8}{12.5}) \\ ∠ Z = {51.63}^{°} \end{array}$

Therefore, $∠ Z$ is approximately 52°.

Now that you’re comfortable with these calculations involving right-angled triangles, you’ll explore some cases where they’re useful in the real world.

Real-world applications

Sometimes in real-world applications, it is necessary to find the measurements of all the sides and angles in a triangle. When an architect designs a set of stairs for a home, they must determine the length, height, and slanted height of the staircase for the plans. The architect must also determine whether the angle of the staircase complies with safety standards. When a builder designs a roof for a sunroom, they must know the dimensions of the roof in order to determine how much building material is needed. They must also determine the slope of the roof for building purposes.

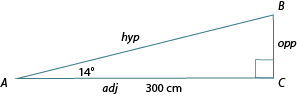
Suppose you want to build a shed. Here is a triangle representing the roof of your shed.

Triangle ABC. Angle A: 14 degrees. Side AC: 300 cm

Let’s determine the measurements of all of the sides and angles in this triangle. This is called “solving the triangle.”

We'll start by labelling the triangle in relation to $∠ A$ , the known angle.

Since we know the measurement of two angles in the triangle, we are able to find the third.

Triangle ABC. Angle A: 14 degrees. Side AC: adj, 300 cm. AB: hyp. BC: opp

Think

What fact lets us calculate the third angle?

The three angles in any triangle add up to 180 degrees.

We can solve for $∠ B$ by subtracting the sum of the two known angles from 180°.

$∠ B = 180 ° - (90 ° + 14 °) = 76 °$

Therefore, $∠ B$ is 76°.

Since there are two unknown sides in the triangle, we must decide which one we want to solve for first. There is no right or wrong answer – we can choose either one.

Let's calculate the opposite side first. Since the triangle is labelled in relation to $∠ A$ , we know the adjacent side of the triangle, and wish to find the opposite side. We'll use the tangent ratio.

$\begin{array}{l} \tan A = \frac{o p p}{a d j} \\ \tan 14 ° = \frac{x}{300.0} \\ x = 300.0 (\tan 14 °) \\ x = 74.8 \end{array}$

The opposite side is about 74.8 cm.

Now let’s calculate the hypotenuse. We could use one of the primary trig ratios again, but once we know two of the sides in a right-angled triangle, there is a quicker way to find the measurement of the third side. You may have learned about it in a previous mathematics course. Do you know what it is?

The Pythagorean Theorem

The Pythagorean Theorem is a formula that relates the three sides of a right-angled triangle. If you square the two short sides of the triangle and add these numbers together, it will equal the square of the long side, which is the hypotenuse.

Formula

This is the formula:

$a^{2} + b^{2} = c^{2}$

Note: Where c is the hypotenuse

Disclaimer: The scenario in this video was used to demonstrate the Pythagorean theorem. At all times practice safety and promote safe workplace behaviour when using ladders.

Explore this!

Explore the following two videos for a review of the Pythagorean theorem. As you will learn in these videos, the hypotenuse in the triangle can be labelled either $c$ or $h$ .

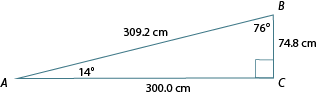
Now let’s calculate the hypotenuse for our roof of a shed example using the Pythagorean theorem.

$\begin{array}{l} a^{2} + b^{2} = c^{2} \\ {(74.8)}^{2} + {(300.0)}^{2} = c^{2} \\ 5,595.04 + 90 000 = c^{2} \\ 95 595.04 = c^{2} or \\ c^{2} = 95 595.04 \\ c = \sqrt{95 595.04} \\ c = 309.2 \end{array}$

The hypotenuse is 309.2 cm.

Here is the complete triangle:

Triangle ABC. Angle A: 14 degrees. B: 76 degrees. Side AC: 300.0 cm. AB: 309.2 cm. BC: 74.8 cm

Notebook

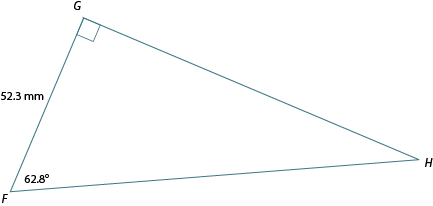
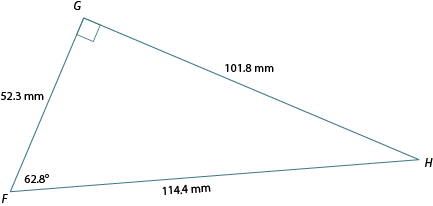
Solve the following triangle in your notebook. (To “solve” a triangle, you must find all missing side lengths and angle measurements). Compare your work with the suggested answers to check your understanding.

Triangle FGH. Angle F: 62.8 degrees. Side FG: 52.3 mm

Step 1

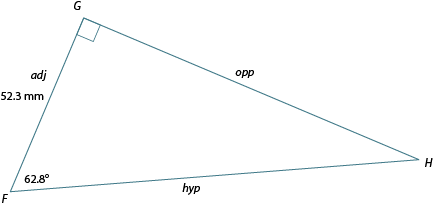
Label the triangle in relation to the given angle.

Triangle FGH. Angle F: 62.8 degrees. Side FG: adj, 52.3 mm. GH: opp. FH: hyp.

Step 2

Solve for $∠ H$ .

$∠ H = 180° - (90° + 62.8°) = 27.2°$

$∠ H$ is 27.2°.

Step 3

Solve for the opposite side.

$\begin{array}{l} \tan A = \frac{o p p}{a d j} \\ \tan 62.8° = \frac{x}{52.3} \\ x = 52.3 (\tan 62.8°) \\ x = 101.8 \end{array}$

The opposite side is about 101.8 mm.

(You could also have chosen to solve for the hypotenuse first.)

Step 4

Solve for the hypotenuse.

$\begin{array}{l} a^{2} + b^{2} = c^{2} \\ {(101.8)}^{2} + {(52.3)}^{2} = c^{2} \\ c^{2} = 13 098.53 \\ c = \sqrt{13 098.53} \\ c = 114.4 \end{array}$

The hypotenuse is about 114.4 mm.

Step 5

Completely label the sides of the triangle.

Triangle FGH. Angle F: 62.8 degrees. Side FG: 52.3 mm. GH: 101.8 mm. FH: 114.4 mm.

In the real world …

Suppose an architect who is designing a staircase between the first and second floor knows the height between floors, but needs to determine the floor space required for the staircase, as well as its slanted height. Ideally, a staircase should be inclined at an angle of 36°. The distance between the two floors is 3.2 m. Find all measurements involved in this triangular design.

Let's draw a right-angled triangle to represent this situation.

Triangle ABC. Angle A: 36 degrees. Angle C:54 degrees. AB: 4.4 m. AC: 5.4 m. BC: 3.2 m

Now we can calculate the length of the staircase using the primary trig ratios.

Since we are labelling the triangle in relation to $∠ A$ , we need a ratio that includes the opposite and adjacent sides.

$\begin{array}{l} \tan A = \frac{o p p}{a d j} \\ \tan 36 ° = \frac{3.2}{x} \\ x = \frac{3.2}{\tan 36 °} \\ x = 4.4 \end{array}$

The staircase must be 4.4 m in length.

Let’s solve for the hypotenuse or slanted height of the stairs.

Now that we know two of the sides of the triangle, we can use the Pythagorean theorem to solve for the third side.

$\begin{array}{l} a^{2} + b^{2} = c^{2} \\ {(4.4)}^{2} + {(3.2)}^{2} = c^{2} \\ c^{2} = 29.6 \\ c = \sqrt{29.6} \\ c = 5.4 \end{array}$

The slanted height of the stairs is approximately 5.4 m.

Here is the complete triangle representing the staircase:

Notebook

You can use your notebook to complete each of the following questions. Compare your work with the suggested answers to check your understanding. Keep in mind that you need to include units in your final answers.

A homeowner would like to build a sunroom on the back of his house and has chosen to build a lean-to roof. The dimensions of the sunroom are 4.0 m by 4.0 m. The roof is inclined at an angle of 18°.

Sun room addition on top of a brick back porch

Draw a labelled diagram to model the roof.
Solve the triangle.
Calculate the surface area of the roof.
Calculate the cost of shingles if they are $10 per square metre (m²).

Step 1

Here is the labelled diagram to model the roof.

Triangle ABC. Angle A: 18 degrees. Side AB: 4.0 mm.

Step 2

Solve for the hypotenuse of the triangle:

$\begin{array}{l} \cos A = \frac{a d j}{h y p} \\ \cos 18 ° = \frac{4.0}{x} \\ x = \frac{4.0}{\cos 18 °} \\ x = 4.2 \end{array}$

Therefore, the hypotenuse is approximately 4.2 m.

Solve for the opposite side of the triangle.

$\begin{array}{l} a^{2} + b^{2} = c^{2} \\ a^{2} + {(4.0)}^{2} = {(4.2)}^{2} \\ a^{2} + 16.00 = 17.64 \\ a^{2} = 17.64 - 16.00 \\ a^{2} = 1.64 \\ a = \sqrt{1.64} \\ a = 1.28 \\ The opposite side of the triangle is about 1.3 m . \end{array}$

Step 3

Solve for $∠ C$ .

$∠ C = 100 ° - (90 ° + 18 °) = 72 °$

$∠ C$ is 72°.

This is the complete triangle:

Triangle ABC. Angle A: 18 degrees. Angle C: 72 degrees. AB: 4.0 m. AC: 5.4 m. BC: 1.3 m. AC: 4.2 m.

Step 4

The width of the roof is the same as the width of the room, so 4.0 m.

We know the slanted height of the roof is 4.2 m from Step 2.

The surface area of the roof is (4.2 m)×(4.0 m) = 16.8 m²

Step 5

To find the cost of the shingles, we must multiply 16.8 square metres by the price per square metre for the shingles.

16.8 × $10 = $168.00.

The cost of the shingles is $168.00.

This example demonstrates that in the world of architecture and construction, you need to be able to perform calculations involving right-angled triangles!

Portfolio

Math Journal

In your math journal, summarize how to solve a right triangle. Be sure to discuss the three primary trigonometric ratios. Include evidence of your learning with examples, pictures, and/or explanations.